Spectral Properties of Elementwise-Transformed Spiked Matrices

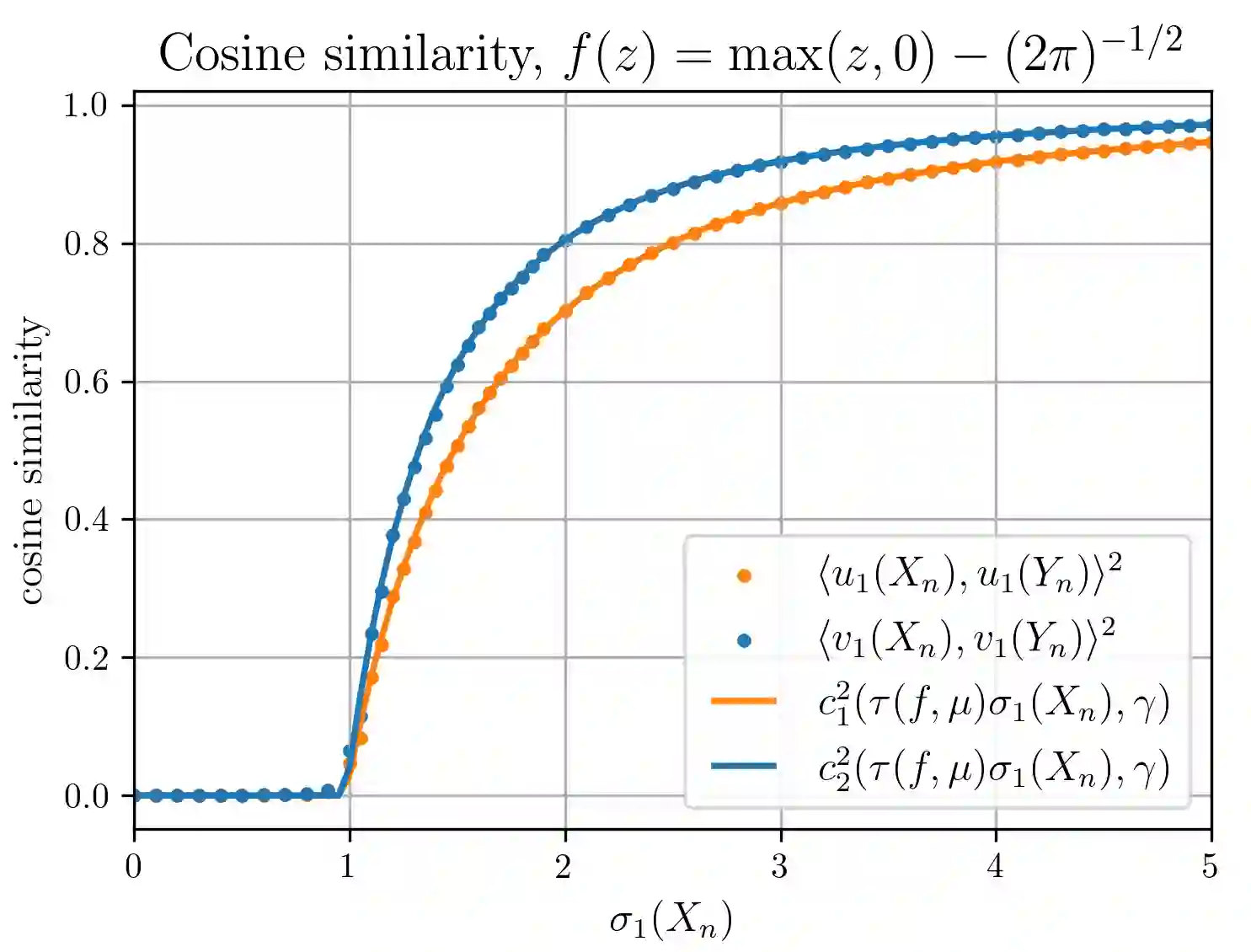
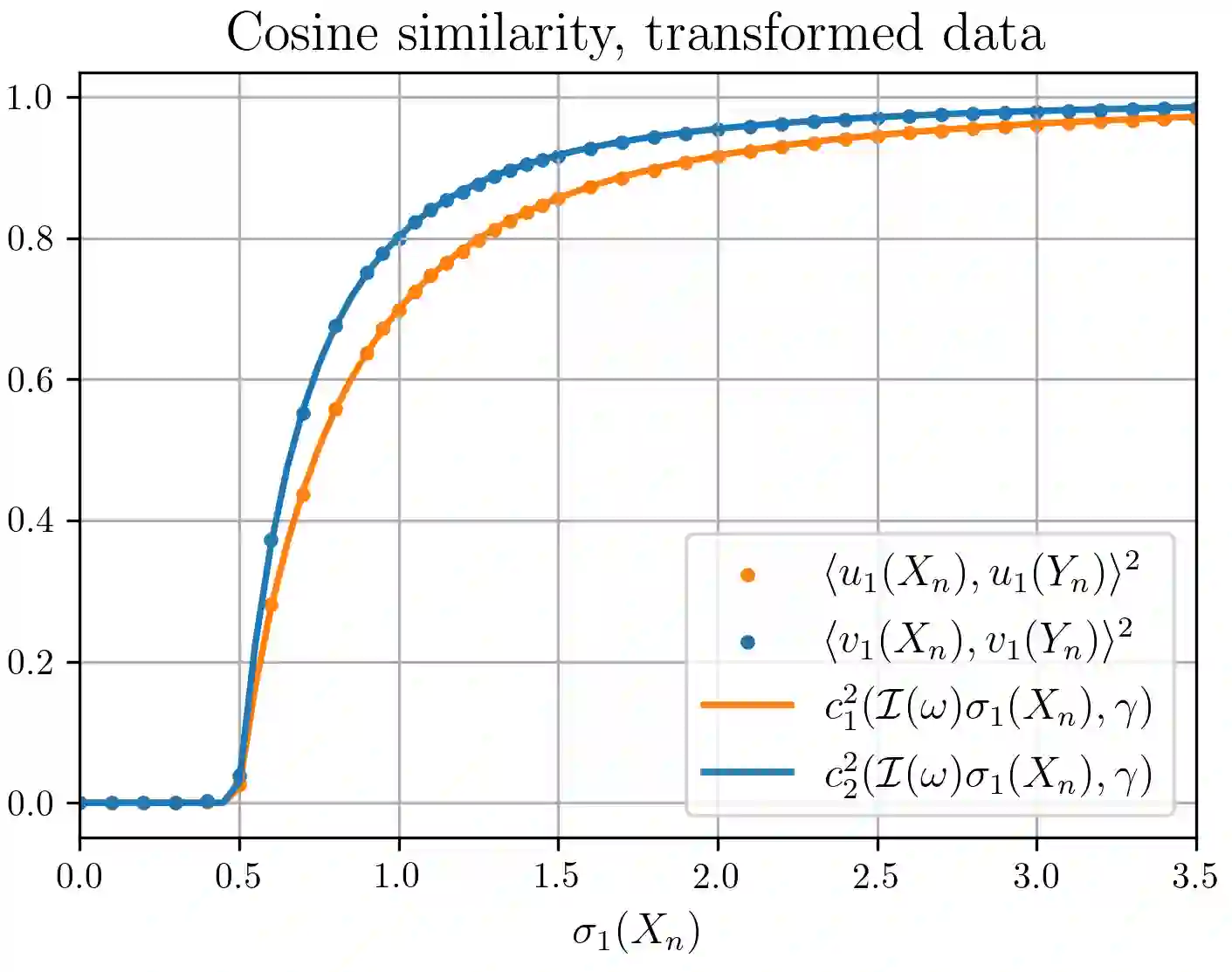
This work concerns elementwise-transformations of spiked matrices: $Y_n = n^{-1/2} f(n^{1-1/(2\ell_*)} X_n + Z_n)$. Here, $f$ is a function applied elementwise, $X_n$ is a low-rank signal matrix, $Z_n$ is white noise, and $\ell_* \geq 1$ is an integer. We find that principal component analysis is powerful for recovering low-rank signal under highly non-linear and discontinuous transformations. Specifically, in the high-dimensional setting where $Y_n$ is of size $n \times p$ with $n,p \rightarrow \infty$ and $p/n \rightarrow \gamma \in (0, \infty)$, we uncover a phase transition: for signal-to-noise ratios above a sharp threshold -- depending on $f$, the distribution of elements of $Z_n$, and the limiting aspect ratio $\gamma$ -- the principal components of $Y_n$ (partially) recover those of $X_n$. Below this threshold, the principal components are asymptotically orthogonal to the signal. In contrast, in the standard setting where $X_n + n^{-1/2}Z_n$ is observed directly, the analogous phase transition depends only on $\gamma$. Analogous phenomena occur with $X_n$ square and symmetric and $Z_n$ a generalized Wigner matrix.