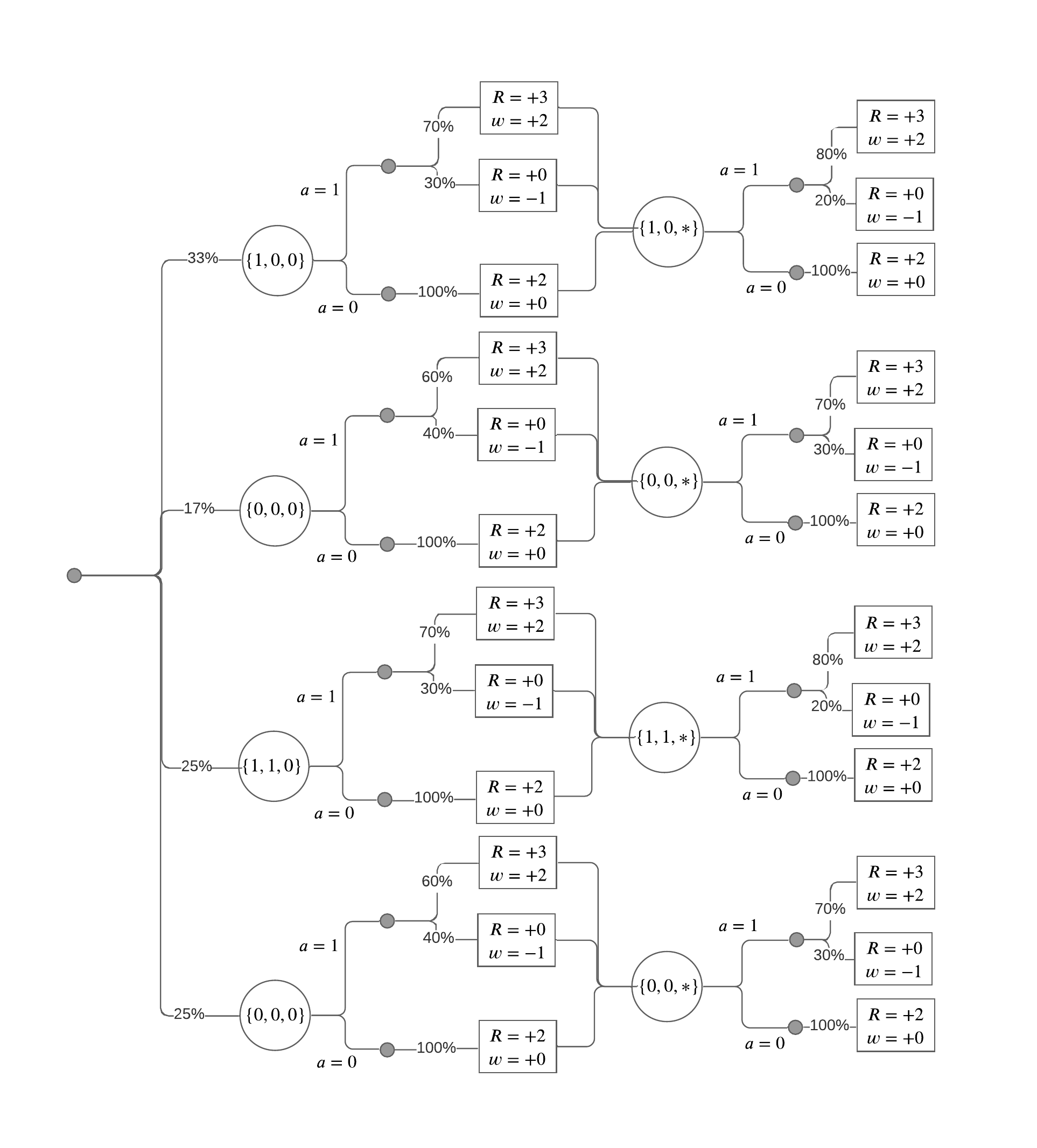
Group fairness definitions such as Demographic Parity and Equal Opportunity make assumptions about the underlying decision-problem that restrict them to classification problems. Prior work has translated these definitions to other machine learning environments, such as unsupervised learning and reinforcement learning, by implementing their closest mathematical equivalent. As a result, there are numerous bespoke interpretations of these definitions. Instead, we provide a generalized set of group fairness definitions that unambiguously extend to all machine learning environments while still retaining their original fairness notions. We derive two fairness principles that enable such a generalized framework. First, our framework measures outcomes in terms of utilities, rather than predictions, and does so for both the decision-algorithm and the individual. Second, our framework considers counterfactual outcomes, rather than just observed outcomes, thus preventing loopholes where fairness criteria are satisfied through self-fulfilling prophecies. We provide concrete examples of how our counterfactual utility fairness framework resolves known fairness issues in classification, clustering, and reinforcement learning problems. We also show that many of the bespoke interpretations of Demographic Parity and Equal Opportunity fit nicely as special cases of our framework.
翻译:诸如人口均等和平等机会等群体公平定义对限制其分类问题的基本决策问题作出假设; 先前的工作通过实施最接近的数学等同方法,将这些定义转化为其他机器学习环境,例如无监督的学习和强化学习; 因此,对这些定义有许多自言自语的解释; 相反,我们提供了一套普遍的集体公平定义,明确扩展到所有机器学习环境,同时仍然保留其原有的公平概念; 我们从两个公平原则中得出了这样的普遍框架。 首先,我们的框架衡量结果是公用事业,而不是预测,而且对于决策-等级和个人来说都是如此。 其次,我们的框架考虑反事实的结果,而不是仅仅观察的结果,从而防止通过自我实现预言满足公平标准的漏洞。 我们提供了具体的例子,说明我们反事实的公平框架如何解决分类、组合和强化学习问题等已知的公平问题。 我们还表明,许多关于人口均等和平等机会的直言不讳的解释与我们框架的特殊情况相符。