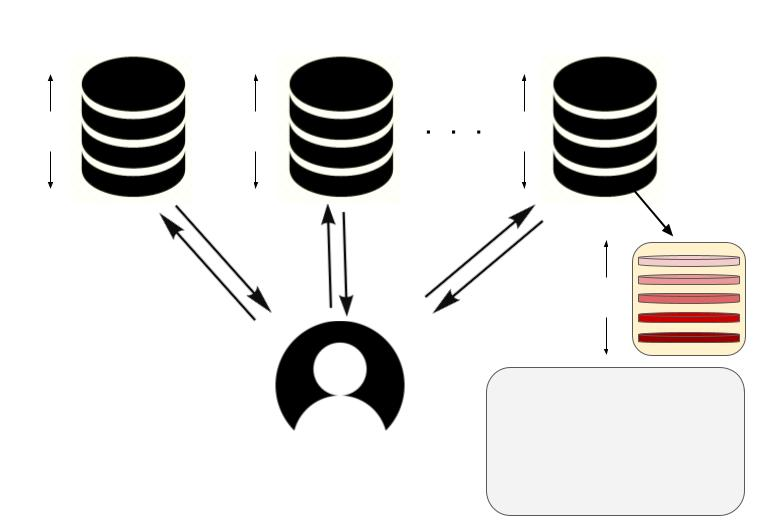
In this paper we study the problem of private information retrieval where a user seeks to retrieve one of the $F$ files from a cluster of $N$ non-colluding servers without revealing the identity of the requested file. In our setting the servers are storage constrained in that they can only store a fraction $\mu=t/N$ of each file. Furthermore, we assume that the files are stored in an uncoded fashion. The rate of a PIR protocol is defined as the ratio of the file size and the total number of bits downloaded. The maximum achievable rate is referred to as capacity. It was previously shown that there are capacity achieving PIR protocols when the file size is $N^F$ and complete files were stored on all the servers. These results were further extended for the case when servers store only a fraction of each file. However, the subpacketization $v$ of the files required is exponential in the number of servers $N$. We propose a novel uncoded PIR protocol based on combinatorial designs that are also capacity achieving when the file size is $v \times t^F$. Our protocol has linear subpacketization in the number of servers in contrast to previous work in storage constrained uncoded PIR schemes. In the proposed PIR protocol, the given system is projected to multiple instances of reduced systems with replicated servers having full storage capacity. The subfiles stored in these various instances are separately retrieved and lifted to solve the PIR problem for the original system.
翻译:在本文中,我们研究私人信息检索问题,即一个用户试图从一组未披露所请求文件身份的“$N$”的未加工服务器中检索一个美元文件,但并不透露所请求文件的身份。在我们的设置中,服务器的存储受到限制,因为只能存储每个文件的一小部分美元=t/N$。此外,我们假设文件以未编码的方式存储。PIR协议的速率被定义为文件大小的比例和下载的比特总数。最大可实现率被称为能力。以前曾显示,当文件大小为$N$F$和完整文件存储在所有服务器上时,就有能力实现PIR协议。当服务器的大小为$v=$和完整时,当服务器的大小为$v=t{F$时,这些结果在服务器只存储每个文件的一小部分时,这些结果被进一步扩展。然而,所需文件的子包装值以未编码的速度在服务器数量上是指数指数指数指数。我们建议,在文件大小为$v=时间t_F$美元时,也可以将P_F$。我们的协议在服务器的原始存储系统里程系统里端系统内,这些存储程序的压缩程序在预定的存储程序上,这些程序在前的压缩的存储系统里端压缩的存储程序程序程序到Pvackropvpvackrocrocrocormadrodrodroldrestral pralal pral pral pral pral pral pressal pral prilal prilal pressal pral prilal prilal pressalal prilal prilal pressalvicilal pral lacutional pressal ladalal ladal ladal ladal sicil sal sal sal sal sal sal sal sal sal sal sal lactional sistral lactional lactional sistral sistralal sicustral lactional pral sireal sireal sireal lactional lactional lactional lactional lactional sireal sireal lactional