Divide-and-Conquer: A Distributed Hierarchical Factor Approach to Modeling Large-Scale Time Series Data

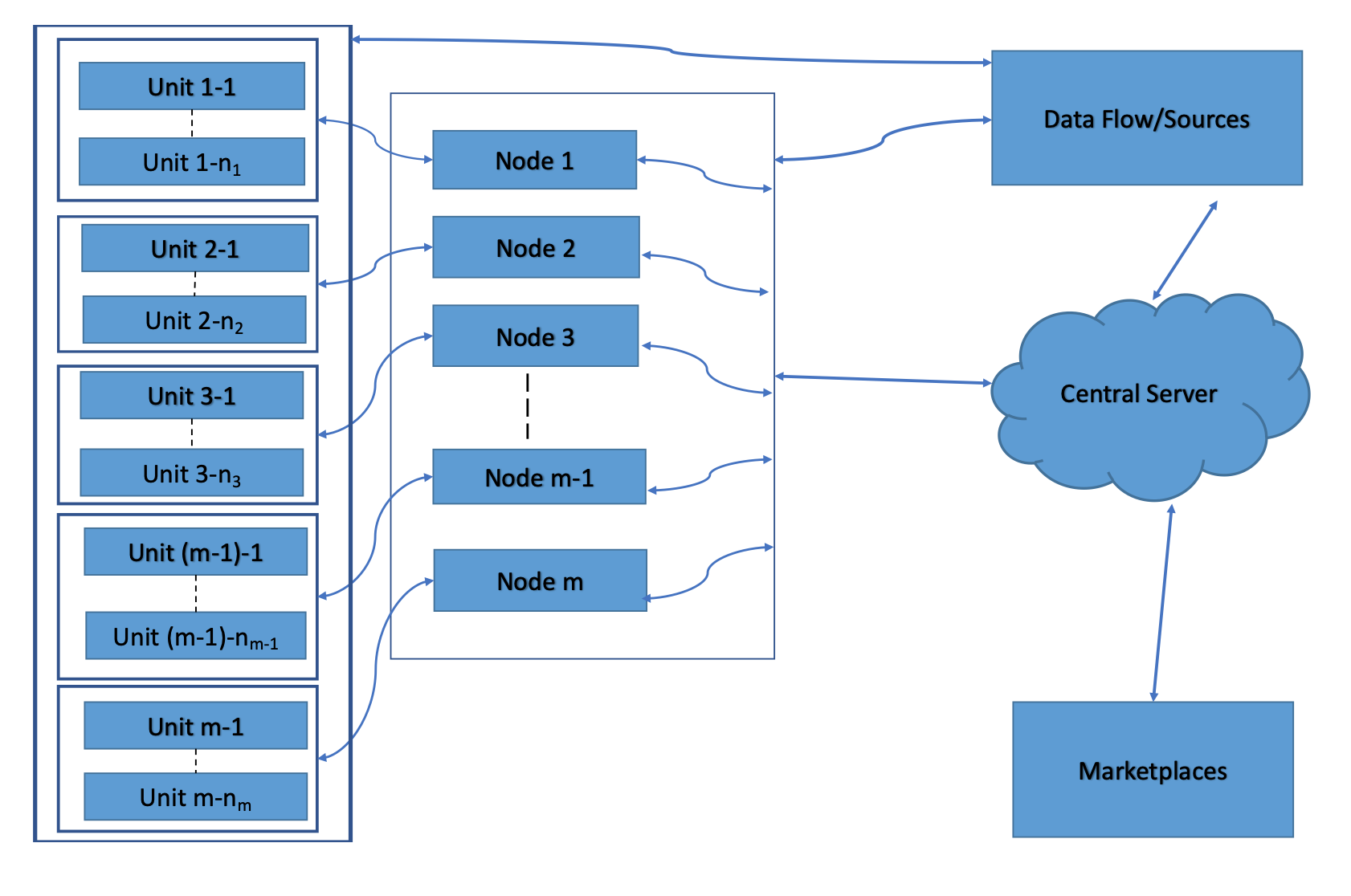
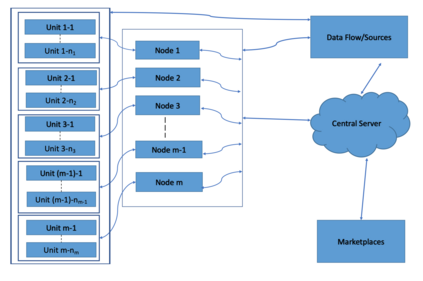
This paper proposes a hierarchical approximate-factor approach to analyzing high-dimensional, large-scale heterogeneous time series data using distributed computing. The new method employs a multiple-fold dimension reduction procedure using Principal Component Analysis (PCA) and shows great promises for modeling large-scale data that cannot be stored nor analyzed by a single machine. Each computer at the basic level performs a PCA to extract common factors among the time series assigned to it and transfers those factors to one and only one node of the second level. Each 2nd-level computer collects the common factors from its subordinates and performs another PCA to select the 2nd-level common factors. This process is repeated until the central server is reached, which collects common factors from its direct subordinates and performs a final PCA to select the global common factors. The noise terms of the 2nd-level approximate factor model are the unique common factors of the 1st-level clusters. We focus on the case of 2 levels in our theoretical derivations, but the idea can easily be generalized to any finite number of hierarchies. We discuss some clustering methods when the group memberships are unknown and introduce a new diffusion index approach to forecasting. We further extend the analysis to unit-root nonstationary time series. Asymptotic properties of the proposed method are derived for the diverging dimension of the data in each computing unit and the sample size $T$. We use both simulated data and real examples to assess the performance of the proposed method in finite samples, and compare our method with the commonly used ones in the literature concerning the forecastability of extracted factors.