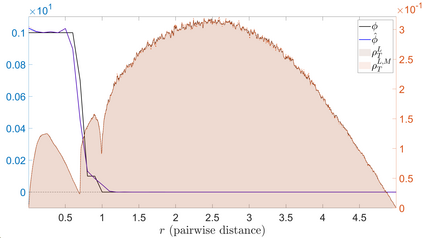
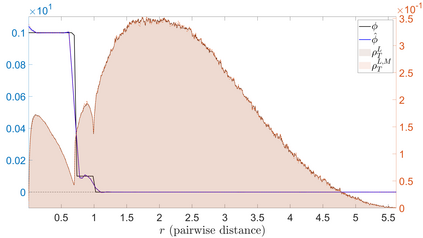
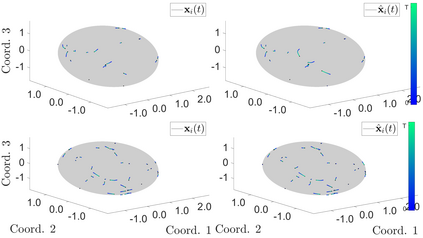
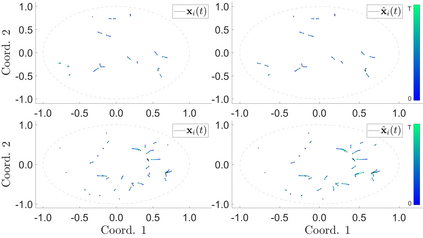
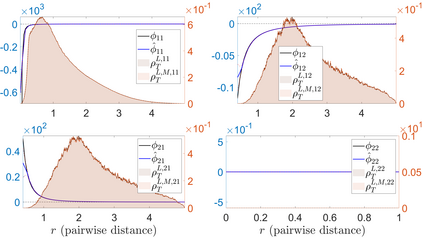
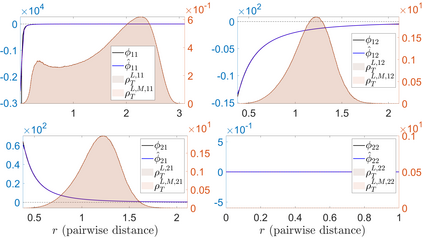
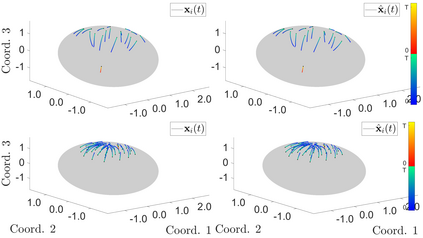
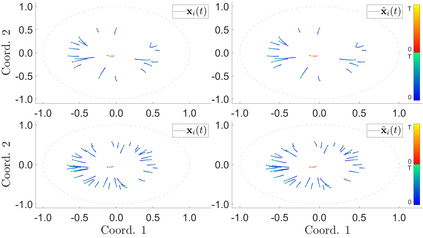
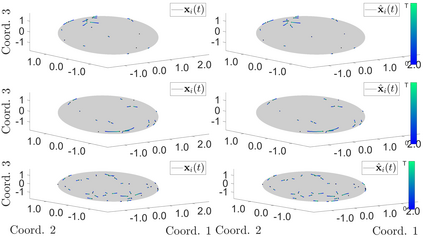
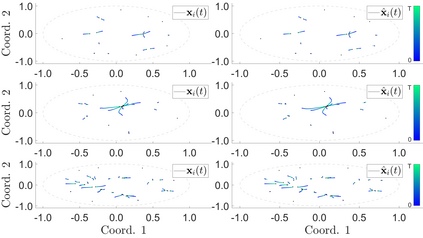
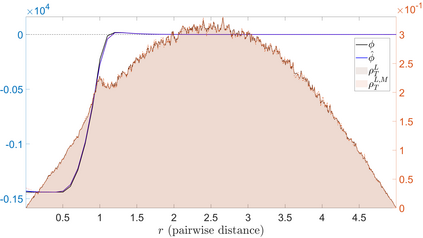
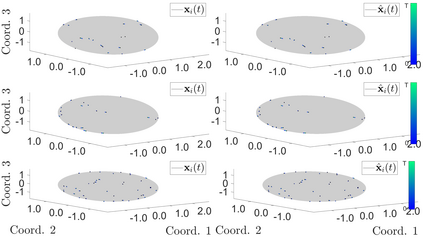
Interacting agent and particle systems are extensively used to model complex phenomena in science and engineering. We consider the problem of learning interaction kernels in these dynamical systems constrained to evolve on Riemannian manifolds from given trajectory data. The models we consider are based on interaction kernels depending on pairwise Riemannian distances between agents, with agents interacting locally along the direction of the shortest geodesic connecting them. We show that our estimators converge at a rate that is independent of the dimension of the state space, and derive bounds on the trajectory estimation error, on the manifold, between the observed and estimated dynamics. We demonstrate the performance of our estimator on two classical first order interacting systems: Opinion Dynamics and a Predator-Swarm system, with each system constrained on two prototypical manifolds, the $2$-dimensional sphere and the Poincar\'e disk model of hyperbolic space.
翻译:互换剂和粒子系统被广泛用于模拟科学和工程的复杂现象。 我们考虑了这些动态系统中学习互动内核的问题,这些动态系统中的内核只能从特定轨道数据中从里曼式的方块上演进。 我们所考虑的模型是基于根据代理人之间对齐的里曼式距离而进行互动的内核,其中代理物沿着最短的大地测量仪的方向在当地进行互动。 我们显示,我们的测算器在不受国家空间维度影响的速率上汇合,并且从所观测到的和估计的动态的方块上的轨误差中得出界限。 我们展示了我们的测算器在两种经典第一顺序互动系统中的性能:意见动态和捕捉者-斯温系统,每个系统都受两种原型的外形元体、两美元的维维空间和双曲空间的波因卡尔磁盘模型的限制。