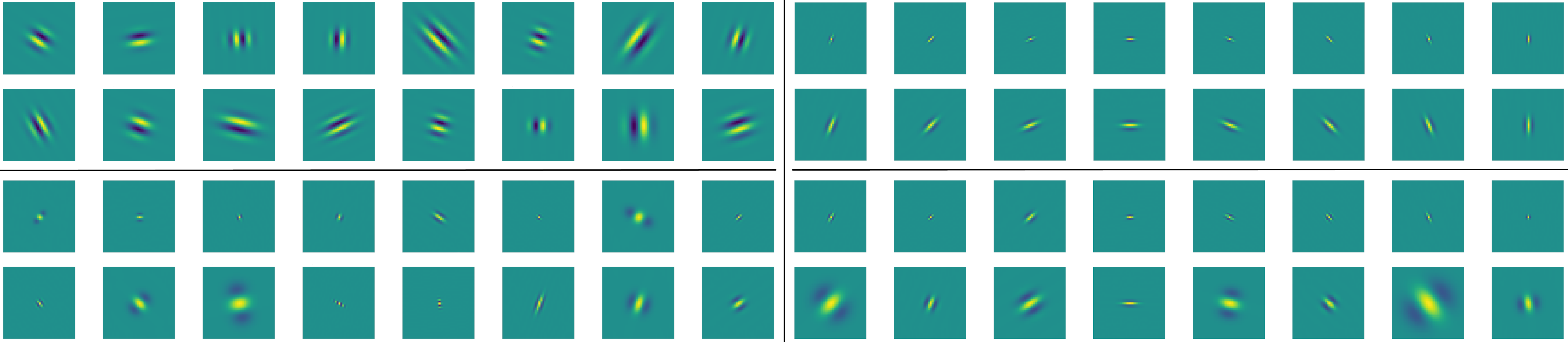
The wavelet scattering transform creates geometric invariants and deformation stability from an initial structured signal. In multiple signal domains it has been shown to yield more discriminative representations compared to other non-learned representations, and to outperform learned representations in certain tasks, particularly on limited labeled data and highly structured signals. The wavelet filters used in the scattering transform are typically selected to create a tight frame via a parameterized mother wavelet. Focusing on Morlet wavelets, we propose to instead adapt the scales, orientations, and slants of the filters to produce problem-specific parametrizations of the scattering transform. We show that our learned versions of the scattering transform yield significant performance gains over the standard scattering transform in the small sample classification settings, and our empirical results suggest that tight frames may not always be necessary for scattering transforms to extract effective representations.
翻译:散落的波子变换会从初始结构化信号中产生几何变异和变形稳定性。 在多个信号域中,显示它与其他非学习的表示相比,产生更具歧视性的表示方式,在某些任务中表现优于所学的表示方式,特别是在有限的标签数据和高度结构化的信号方面。 散落变换中使用的波子过滤器通常被选为通过参数化母波子建立紧身框架。 聚焦于摩尔特波子,我们提议对过滤器的尺寸、方向和倾斜进行调整,以产生分散变异的偏差。 我们显示,我们所学的分散变异版本在小样本分类设置的标准分散变异方面产生显著的性能收益,我们的经验结果表明,为了提取有效的表达方式,分散变异的变形不一定需要紧身框架。