The Expectation-Maximization Algorithm for Continuous-time Hidden Markov Models

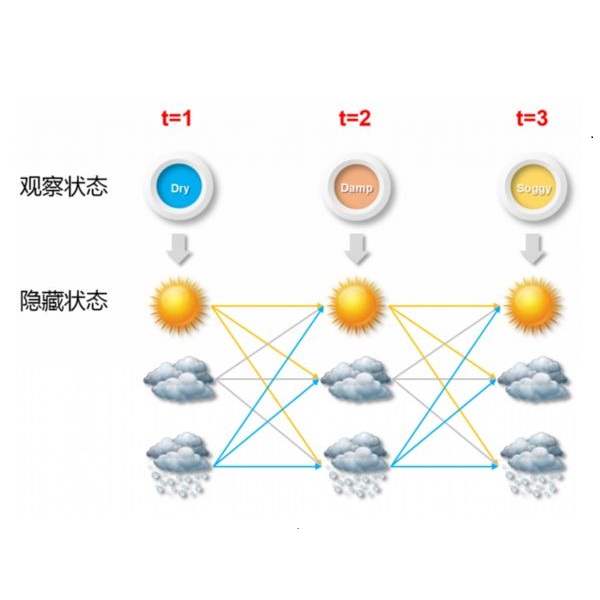
We propose a unified framework that extends the inference methods for classical hidden Markov models to continuous settings, where both the hidden states and observations occur in continuous time. Two different settings are analyzed: (1) hidden jump process with a finite state space; (2) hidden diffusion process with a continuous state space. For each setting, we first estimate the hidden state given the observations and model parameters, showing that the posterior distribution of the hidden states can be described by differential equations in continuous time. Then we consider the estimation of unknown model parameters, deriving the formulas for the expectation-maximization algorithm in the continuous-time setting. We also propose a Monte Carlo method for sampling the posterior distribution of the hidden states and estimating the unknown parameters.