Convergence of a Lagrangian discretization for barotropic fluids and porous media flow

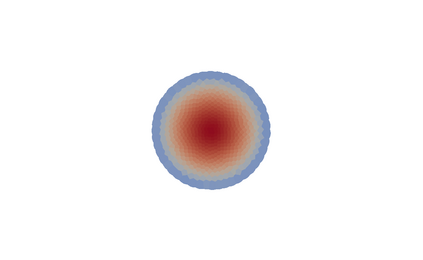
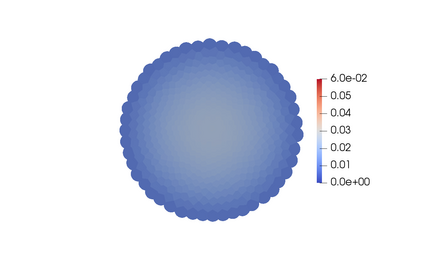
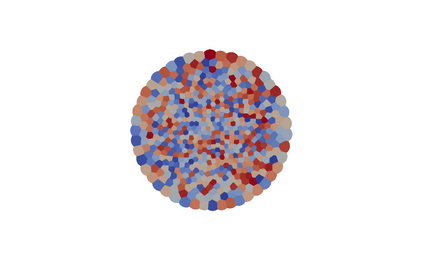
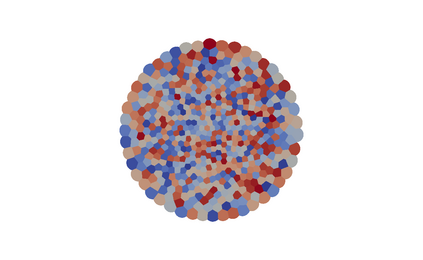
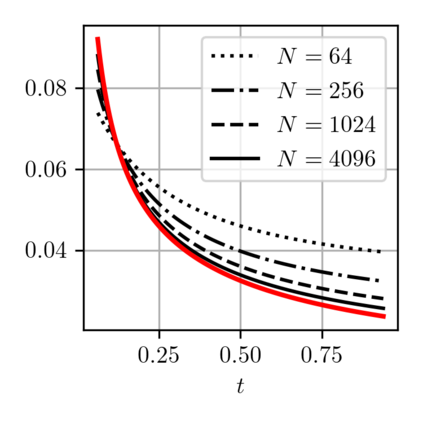
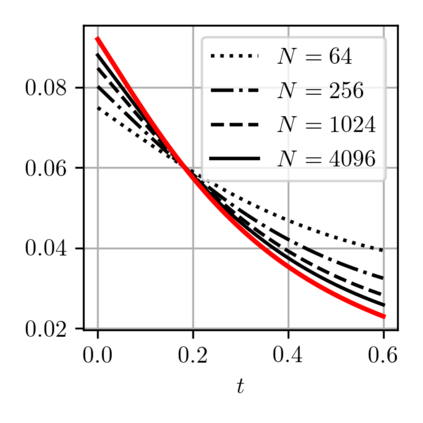
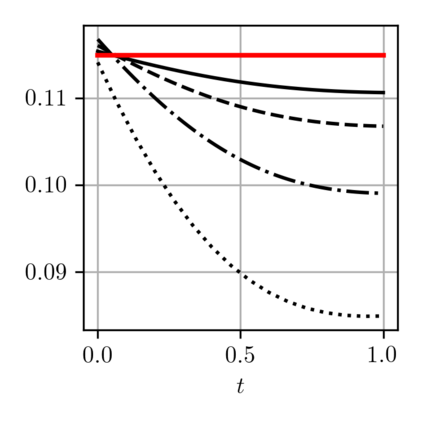
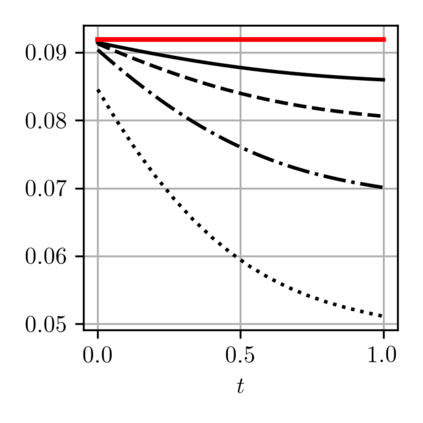
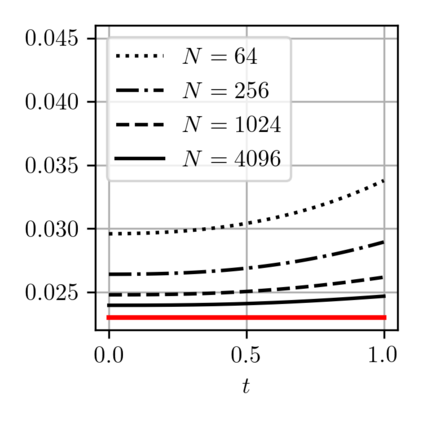
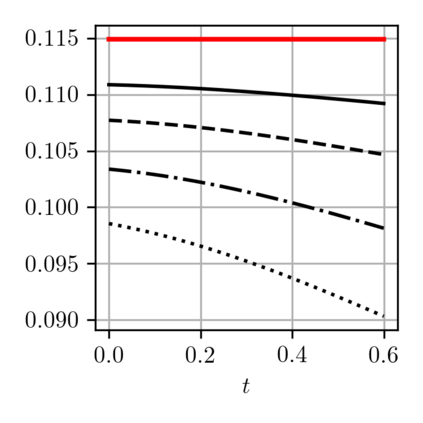
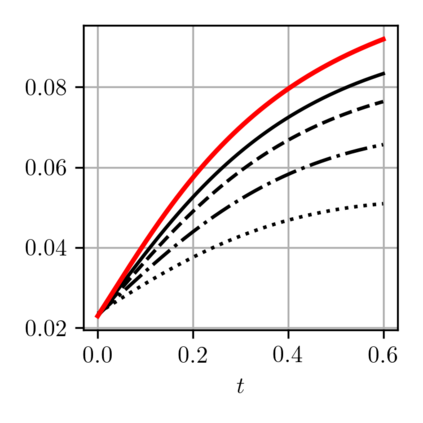
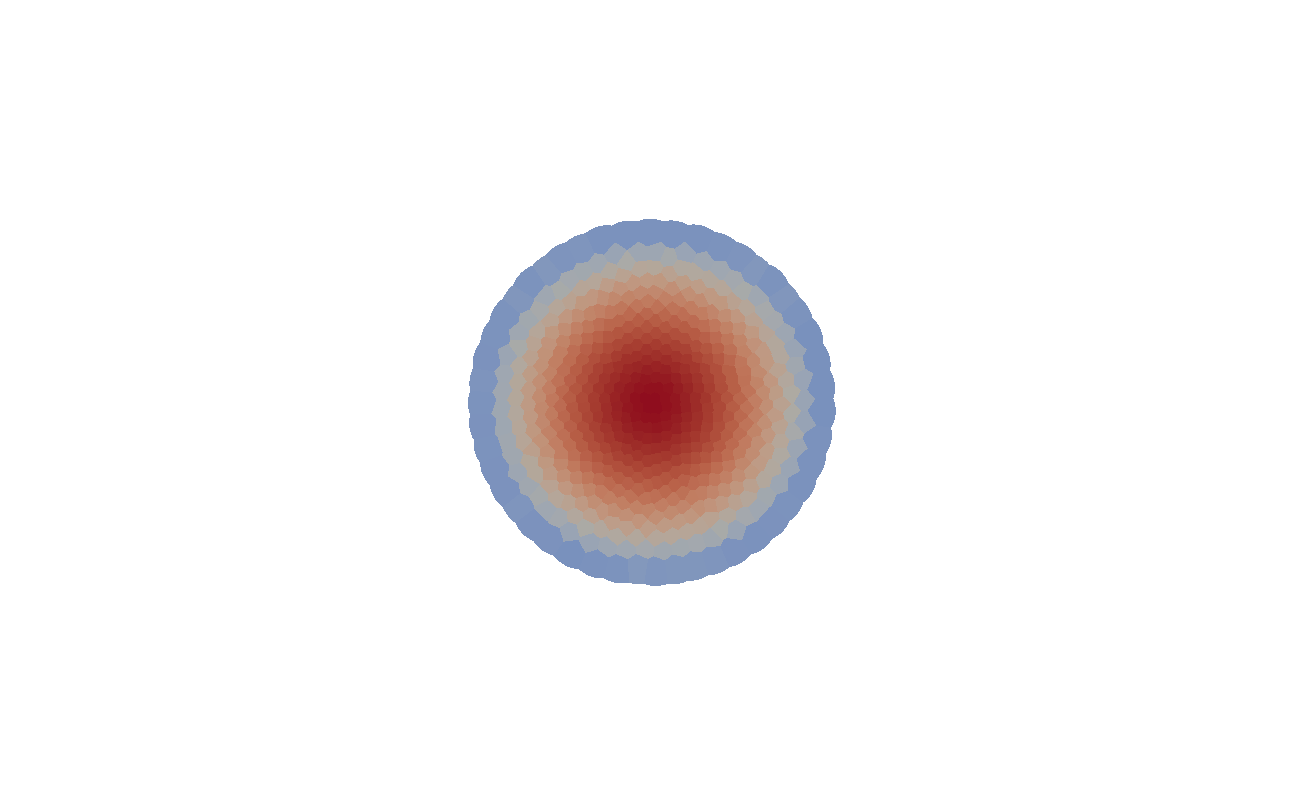
When expressed in Lagrangian variables, the equations of motion for compressible (barotropic) fluids have the structure of a classical Hamiltonian system in which the potential energy is given by the internal energy of the fluid. The dissipative counterpart of such a system coincides with the porous medium equation, which can be cast in the form of a gradient flow for the same internal energy. Motivated by these related variational structures, we propose a particle method for both problems in which the internal energy is replaced by its Moreau-Yosida regularization in the L2 sense, which can be efficiently computed as a semi-discrete optimal transport problem. Using a modulated energy argument which exploits the convexity of the problem in Eulerian variables, we prove quantitative convergence estimates towards smooth solutions. We verify such estimates by means of several numerical tests.