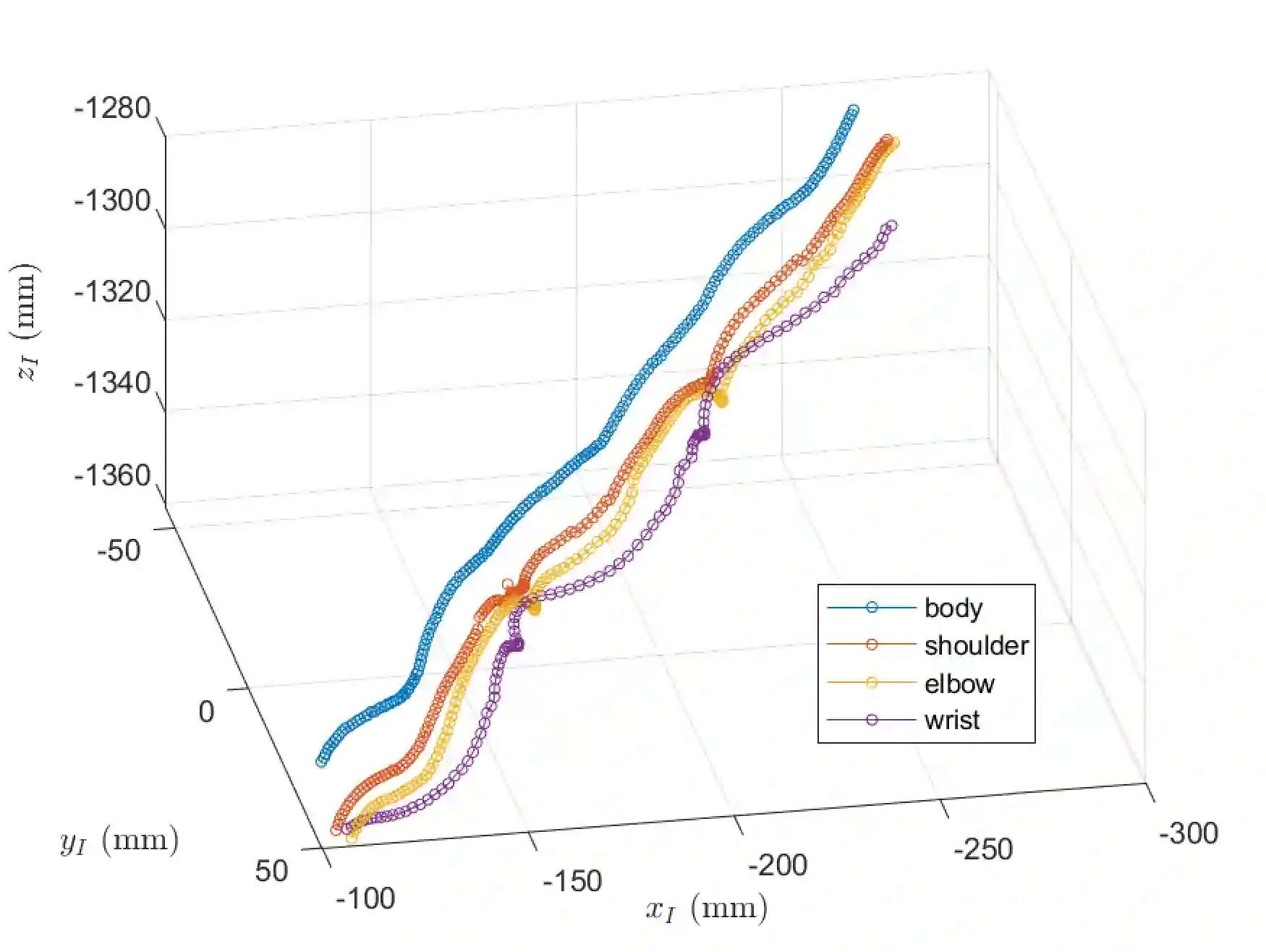
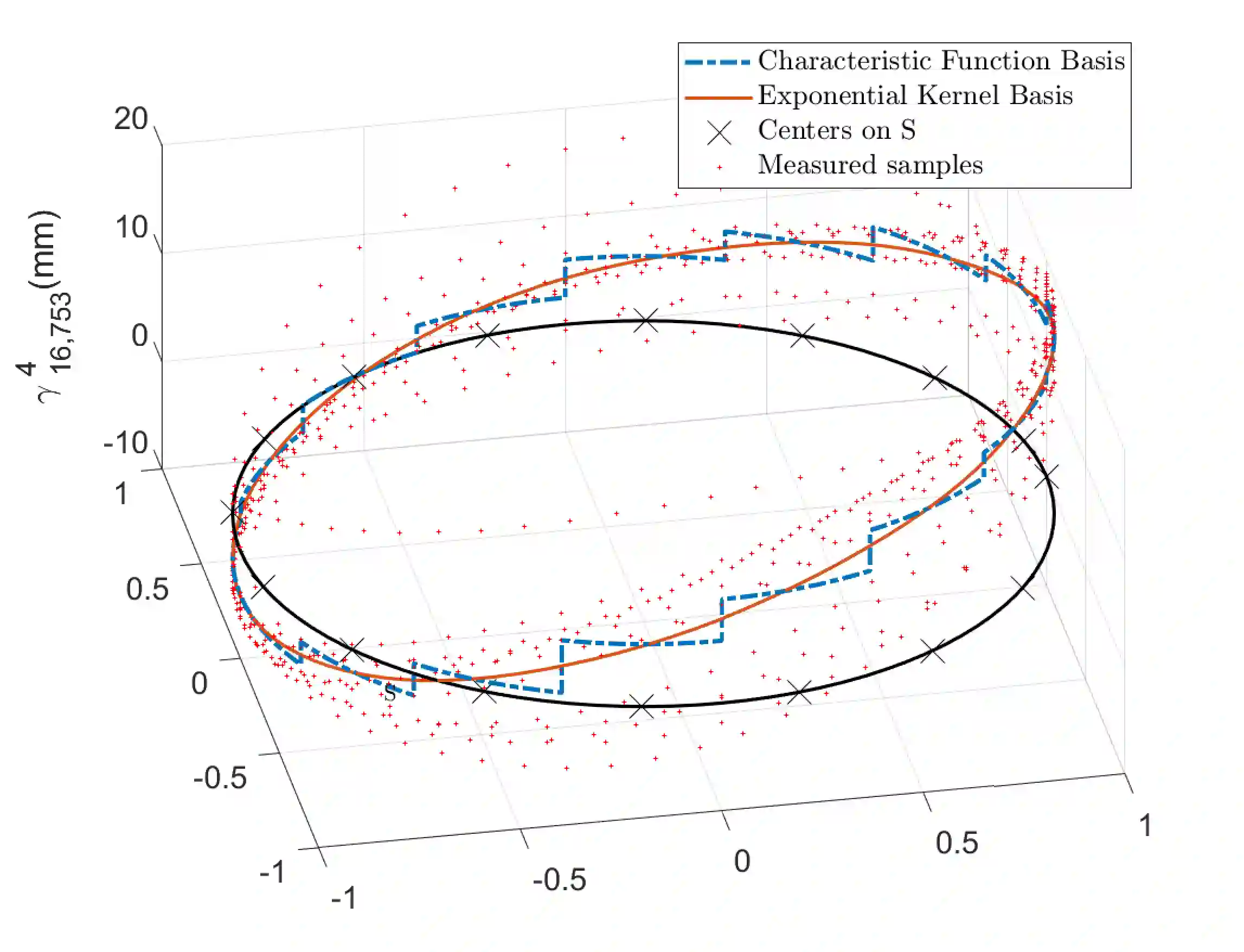
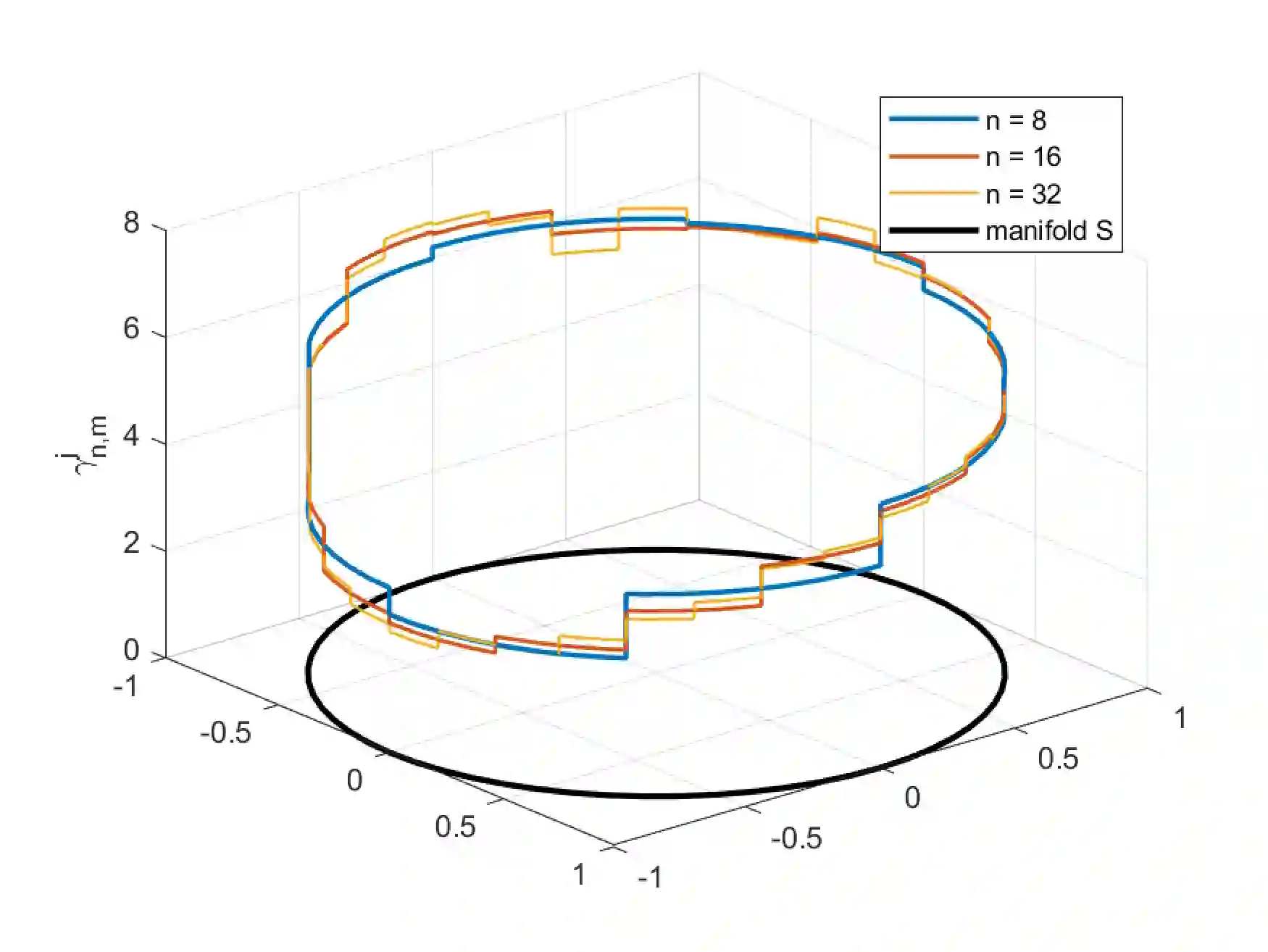
This paper describes the formulation and experimental testing of a novel method for the estimation and approximation of submanifold models of animal motion. It is assumed that the animal motion is supported on a configuration manifold $Q$ that is a smooth, connected, regularly embedded Riemannian submanifold of Euclidean space $X\approx \mathbb{R}^d$ for some $d>0$, and that the manifold $Q$ is homeomorphic to a known smooth, Riemannian manifold $S$. Estimation of the manifold is achieved by finding an unknown mapping $\gamma:S\rightarrow Q\subset X$ that maps the manifold $S$ into $Q$. The overall problem is cast as a distribution-free learning problem over the manifold of measurements $\mathbb{Z}=S\times X$. That is, it is assumed that experiments generate a finite sets $\{(s_i,x_i)\}_{i=1}^m\subset \mathbb{Z}^m$ of samples that are generated according to an unknown probability density $\mu$ on $\mathbb{Z}$. This paper derives approximations $\gamma_{n,m}$ of $\gamma$ that are based on the $m$ samples and are contained in an $N(n)$ dimensional space of approximants. The paper defines sufficient conditions that shows that the rates of convergence in $L^2_\mu(S)$ correspond to those known for classical distribution-free learning theory over Euclidean space. Specifically, the paper derives sufficient conditions that guarantee rates of convergence that have the form $$\mathbb{E} \left (\|\gamma_\mu^j-\gamma_{n,m}^j\|_{L^2_\mu(S)}^2\right )\leq C_1 N(n)^{-r} + C_2 \frac{N(n)\log(N(n))}{m}$$for constants $C_1,C_2$ with $\gamma_\mu:=\{\gamma^1_\mu,\ldots,\gamma^d_\mu\}$ the regressor function $\gamma_\mu:S\rightarrow Q\subset X$ and $\gamma_{n,m}:=\{\gamma^1_{n,j},\ldots,\gamma^d_{n,m}\}$.
翻译:本文描述用于估算和近似动物运动的亚平面模型的新方法的配制和实验测试 。 假设动物运动以一个配置值 $$Q 支持动物运动, 该配置值是平滑的, 连接的, 定期嵌入 Euclidean 空间的里曼尼亚子折叠 $X\ approx\ mathbb{R ⁇ d$ 约美元, 并且, 数Q$是已知的平滑的, Rielmann 元( Ri) 。 通过找到一个未知的映射值 $: S\rightro subset 美元 美元 美元 。 总体问题被描绘成一个不分发的学习问题 $\ aprob_ Stime1, 美元。 也就是说, 假设实验产生的定值 $( s_i, x_i) = 1\\\\\\ om\ coom=xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx