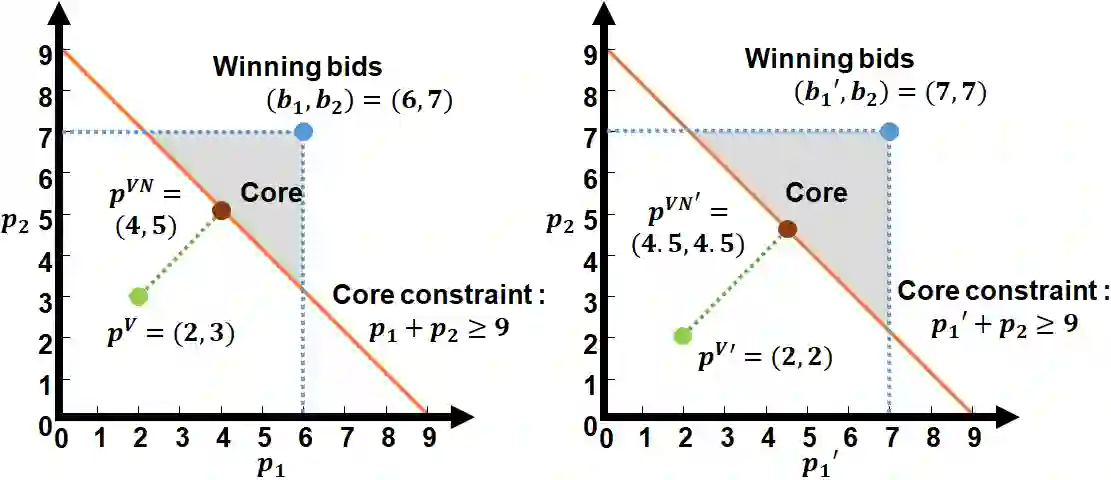
Combinatorial auctions (CAs) allow bidders to express complex preferences for bundles of goods being auctioned. However, the behavior of bidders under different payment rules is often unclear. In this paper, we aim to understand how core constraints interact with different core-selecting payment rules. In particular, we examine the natural and desirable non-decreasing property of payment rules, which states that bidders cannot decrease their payments by increasing their bids. Previous work showed that, in general, the widely used VCG-nearest payment rule violates the non-decreasing property in single-minded CAs. We prove that under a single effective core constraint, the VCG-nearest payment rule is non-decreasing. In order to determine in which auctions single effective core constraints occur, we introduce a conflict graph representation of single-minded CAs and find sufficient conditions for the single effective core constraint in CAs. Finally, we study the consequences on the behavior of the bidders and show that no over-bidding exists in any Nash equilibrium for non-decreasing core-selecting payment rules.
翻译:合并拍卖(CAs)允许投标人对被拍卖的一大批货物表示复杂的偏好。然而,不同支付规则下的投标人的行为往往不明确。在本文中,我们的目的是了解核心限制与不同核心选择付款规则如何相互作用。特别是,我们审查了付款规则的自然和可取的不减少财产,其中规定投标人不能通过增加出价而减少付款。先前的工作表明,一般而言,广泛使用的VCG年期付款规则违反了单一心智CA的非减少财产。我们证明,在单一有效核心限制下,VCG年期付款规则是非取消性。为了确定拍卖在哪种拍卖中发生单一有效核心限制,我们用冲突图表来表示单一心的CAA,并为CAs中单一有效核心限制找到充分的条件。最后,我们研究了投标人行为的后果,并表明,在任何纳什均衡中不存在对不取消核心选择付款规则的过分指责。