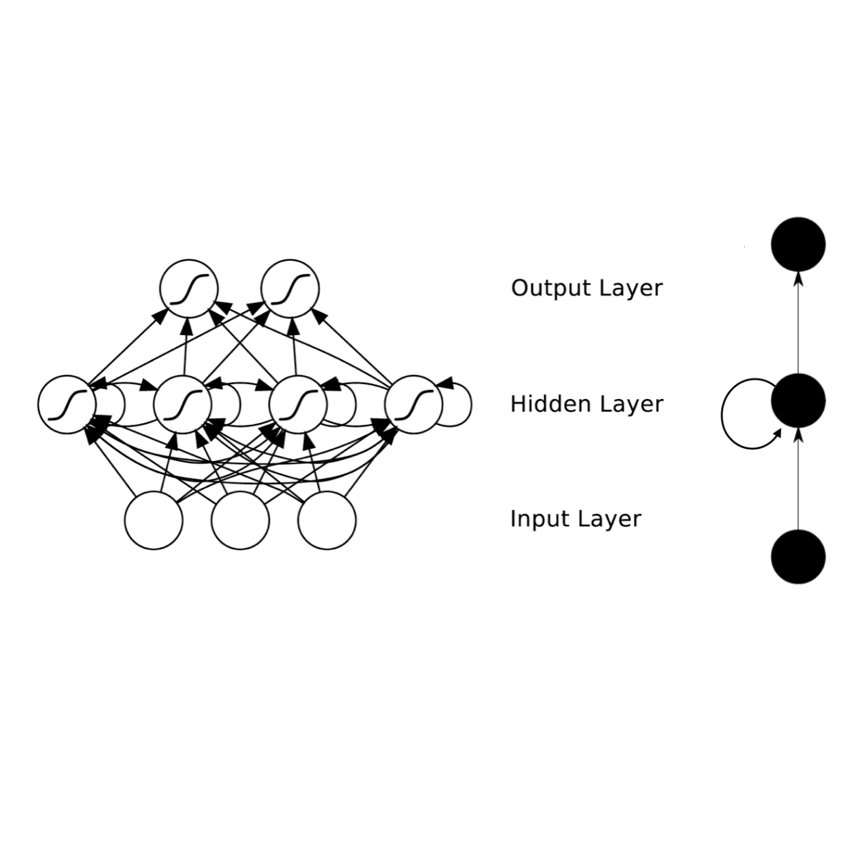
There is a wave of interest in using unsupervised neural networks for solving differential equations. The existing methods are based on feed-forward networks, {while} recurrent neural network differential equation solvers have not yet been reported. We introduce an unsupervised reservoir computing (RC), an echo-state recurrent neural network capable of discovering approximate solutions that satisfy ordinary differential equations (ODEs). We suggest an approach to calculate time derivatives of recurrent neural network outputs without using backpropagation. The internal weights of an RC are fixed, while only a linear output layer is trained, yielding efficient training. However, RC performance strongly depends on finding the optimal hyper-parameters, which is a computationally expensive process. We use Bayesian optimization to efficiently discover optimal sets in a high-dimensional hyper-parameter space and numerically show that one set is robust and can be used to solve an ODE for different initial conditions and time ranges. A closed-form formula for the optimal output weights is derived to solve first order linear equations in a backpropagation-free learning process. We extend the RC approach by solving nonlinear system of ODEs using a hybrid optimization method consisting of gradient descent and Bayesian optimization. Evaluation of linear and nonlinear systems of equations demonstrates the efficiency of the RC ODE solver.
翻译:使用不受监督的神经网络解决差异方程式引起了一波兴趣。 现有的方法基于饲料向向网络, {而经常神经网络差异方程式解决者尚未报告。 我们引入了不受监督的储油层计算(RC),即回声状态的经常性神经网络,能够发现满足普通差异方程式(ODE)的近似解决方案。 我们建议了一种方法来计算经常神经网络输出的经常性神经网络产出的时间衍生物而不使用反向反向偏移法。 RC的内部重量是固定的,而只有线性输出层才受过培训,能够产生有效的培训。 然而, RC的性能在很大程度上取决于找到最佳的超参数,这是一个计算成本高昂的过程。 我们使用Bayesian优化高效地在高维超参数空间中发现最佳的设置。 我们用数字显示,其中一套是坚固的,可以用来在不同的初始条件和时间范围中解析一个运行模式。 最佳输出权重的封闭式公式用于在后向不偏向式学习过程中解第一个顺序线性方方方方程式。 我们利用非线性平流式的中间方程式系统来扩展RC方法, 将标准的升级的升级的升级系统, 升级的升级的升级的升级的系统。