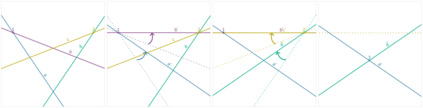
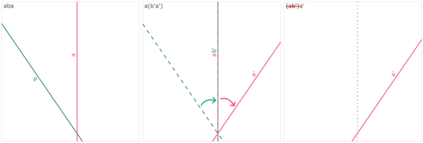
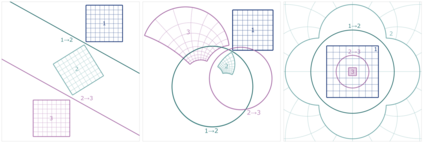
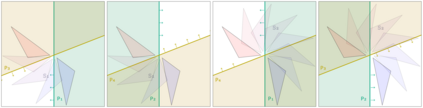
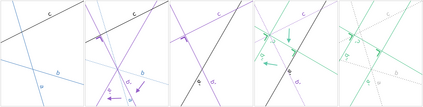
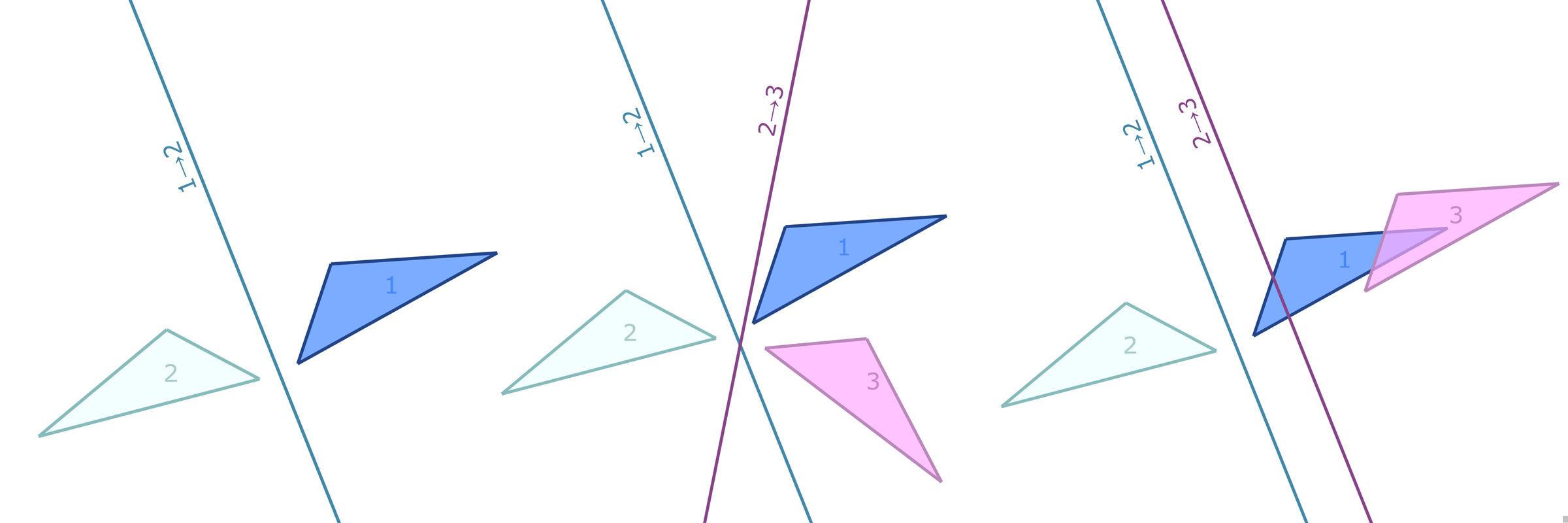
The symmetries described by Pin groups are the result of combining a finite number of discrete reflections in (hyper)planes. The current work shows how an analysis using geometric algebra provides a picture complementary to that of the classic matrix Lie algebra approach, while retaining information about the number of reflections in a given transformation. This imposes a graded structure on Lie groups, which is not evident in their matrix representation. By embracing this graded structure, the invariant decomposition theorem was proven: any composition of $k$ linearly independent reflections can be decomposed into $\lceil k/2 \rceil$ commuting factors, each of which is the product of at most two reflections. This generalizes a conjecture by M. Riesz, and has e.g. the Mozzi-Chasles' theorem as its 3D Euclidean special case. To demonstrate its utility, we briefly discuss various examples such as Lorentz transformations, Wigner rotations, and screw transformations. The invariant decomposition also directly leads to closed form formulas for the exponential and logarithmic function for all Spin groups, and identifies element of geometry such as planes, lines, points, as the invariants of $k$-reflections. We conclude by presenting novel matrix/vector representations for geometric algebras $\mathbb{R}_{pqr}$, and use this in E(3) to illustrate the relationship with the classic covariant, contravariant and adjoint representations for the transformation of points, planes and lines.
翻译:Pin 组描述的对称是将( 超) 平方平面中的离散反射数量有限{ 离散反射组合的结果。 目前的工作显示, 使用几何代数的分析能够提供与经典矩阵 Lie代数法相补充的图片, 同时保留关于特定变换中反射数量的信息。 这给 Lie 组强制设置了一个分级结构, 其矩阵表达方式并不明显。 接受这个分级结构, 证明了不易分解的理论: 任何美元线性独立反射的构成可以解成$lcel k/2\rice$ Screalgeblation 运算要素, 每一种都是两个反射模型的产物。 这一般化了M. Riesz的反射度, 并且将Mozzi- Chasles 的方言作为3Duclideidean 特例。 为了展示它的实用性, 我们简要地讨论各种例子, 比如Lorentz 转换, Wigner 旋调调, 和螺旋值变换值。