Post-Modern GMRES

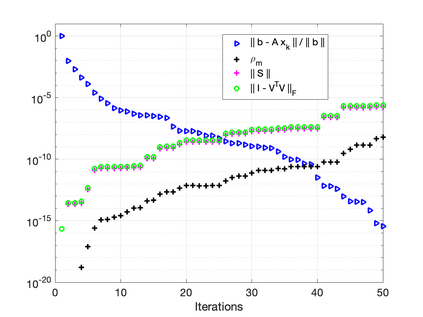
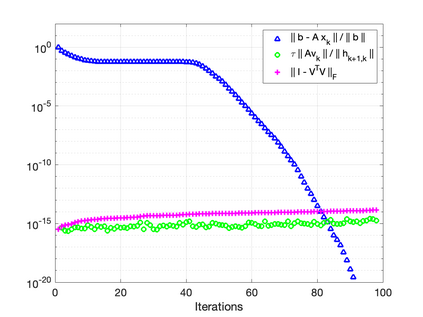
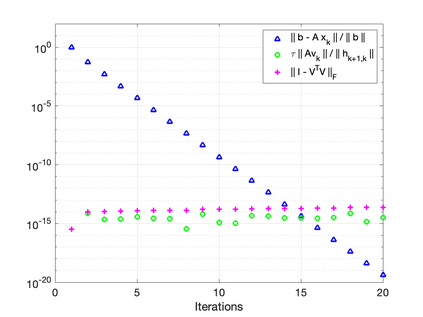
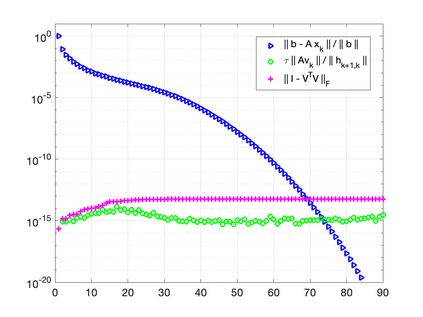
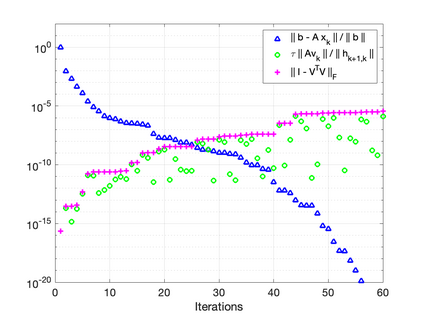
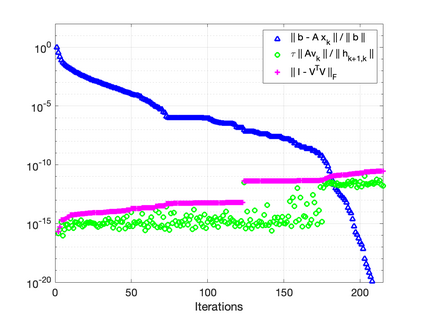
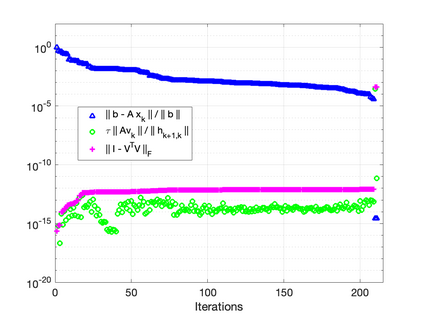
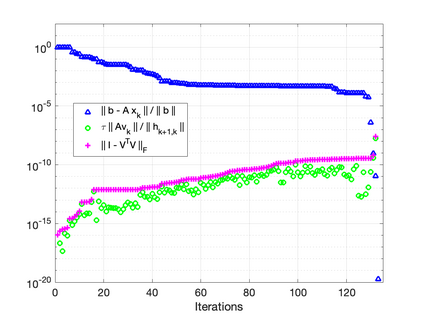
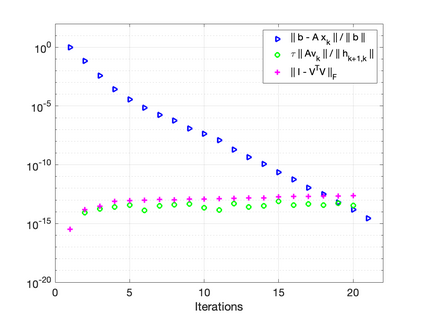
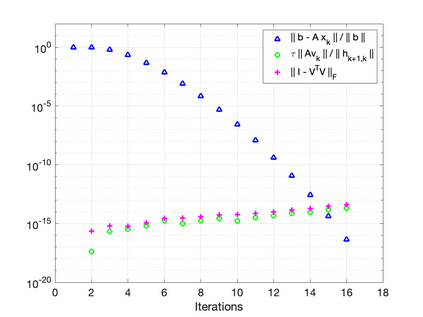
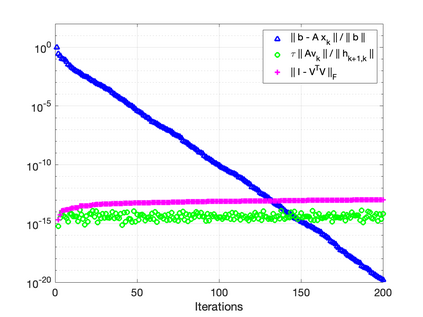
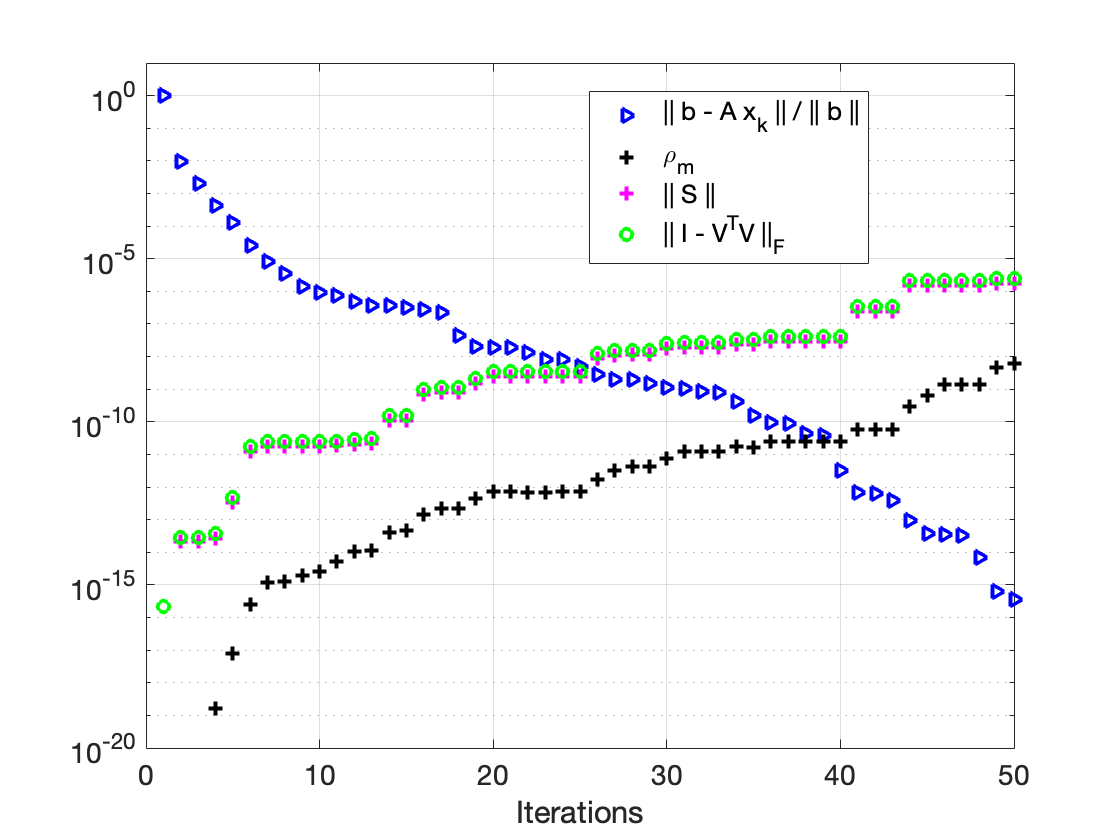
The GMRES algorithm of Saad and Schultz (1986) for nonsymmetric linear systems relies on the Arnoldi expansion of the Krylov basis. The algorithm computes the $QR$ factorization of the matrix $B = [\: {\bf r}_0, AV_k\:]$ at each iteration. Despite an $\mathcal{O}(\epsilon)\kappa(B)$ loss of orthogonality, the modified Gram-Schmidt (MGS) formulation was shown to be backward stable in the seminal papers by Paige, et al. (2006) and Paige and Strako\v{s} (2002). Classical Gram-Schmidt (CGS) exhibits an $\mathcal{O}(\epsilon)\kappa^2(B)$ loss of orthogonality, whereas DCGS-2 (CGS with delayed reorthogonalization) reduces this to $\mathcal{O}(\epsilon)$ in practice (without a formal proof). We present a post-modern (viz. not classical) GMRES algorithm based on Ruhe (1983) and the low-synch algorithms of \'{S}wirydowicz et al (2020) that achieves $\mathcal{O}(\epsilon) \: \|A{\bf v}_k\|_2 /h_{k+1,k}$ loss of orthogonality. By projecting the vector $A{\bf v}_k$, with Gauss-Seidel relaxation, onto the orthogonal complement of the space spanned by the computed Krylov vectors $V_k$ where $V_k^TV_k = I + L_k + L_k^T$, we can further demonstrate that the loss of orthogonality is at most $\mathcal{O}(\epsilon)\kappa(B)$. For a broad class of matrices, unlike MGS-GMRES, significant loss of orthogonality does not occur and the relative residual no longer stagnates for highly non-normal systems. The Krylov vectors remain linearly independent and the smallest singular value of $V_k$ is not far from one. We also demonstrate that Henrici's departure from normality of the lower triangular matrix $T_k \approx (\:V_k^TV_k\:)^{-1}$ in the modified Gram-Schmidt projector $P = I - V_kT_kV_k^T$ is an appropriate quantity for detecting the loss of orthogonality. Our new algorithm results in an almost symmetric correction matrix $T_k$.