Corner asymptotics of the magnetic potential in the eddy-current model

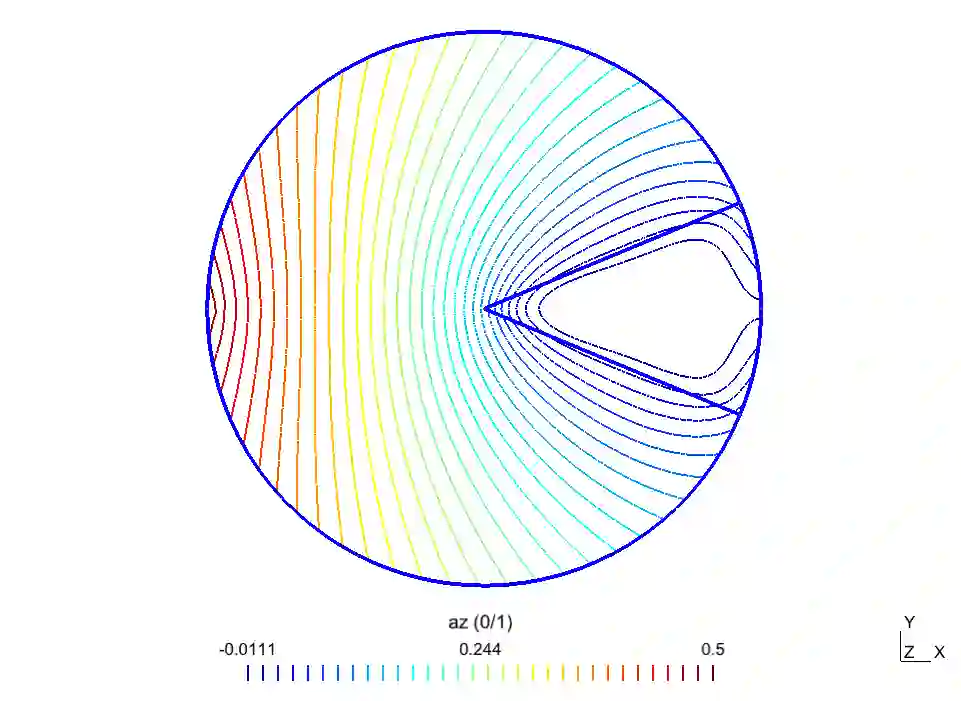
In this paper, we describe the magnetic potential in the vicinity of a corner of a conducting body embedded in a dielectric medium in a bidimensional setting. We make explicit the corner asymptotic expansion for this potential as the distance to the corner goes to zero. This expansion involves singular functions and singular coefficients. We introduce a method for the calculation of the singular functions near the corner and we provide two methods to compute the singular coefficients: the method of moments and the method of quasi-dual singular functions. Estimates for the convergence of both approximate methods are proven. We eventually illustrate the theoretical results with finite element computations. The specific non-standard feature of this problem lies in the structure of its singular functions: They have the form of series whose first terms are harmonic polynomials and further terms are genuine non-smooth functions generated by the piecewise constant zeroth order term of the operator.