Bridging the Usability Gap: Theoretical and Methodological Advances for Spectral Learning of Hidden Markov Models

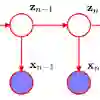
The Baum-Welch (B-W) algorithm is the most widely accepted method for inferring hidden Markov models (HMM). However, it is prone to getting stuck in local optima, and can be too slow for many real-time applications. Spectral learning of HMMs (SHMMs), based on the method of moments (MOM) has been proposed in the literature to overcome these obstacles. Despite its promises, asymptotic theory for SHMM has been elusive, and the long-run performance of SHMM can degrade due to unchecked propogation of error. In this paper, we (1) provide an asymptotic distribution for the approximate error of the likelihood estimated by SHMM, and (2) propose a novel algorithm called projected SHMM (PSHMM) that mitigates the problem of error propogation, and (3) develop online learning variantions of both SHMM and PSHMM that accommodate potential nonstationarity. We compare the performance of SHMM with PSHMM and estimation through the B-W algorithm on both simulated data and data from real world applications, and find that PSHMM not only retains the computational advantages of SHMM, but also provides more robust estimation and forecasting.