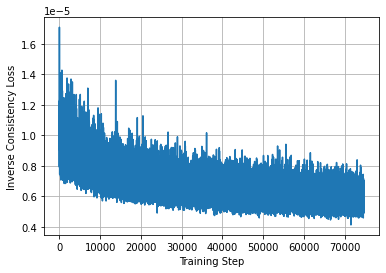
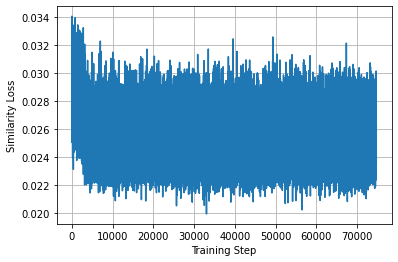
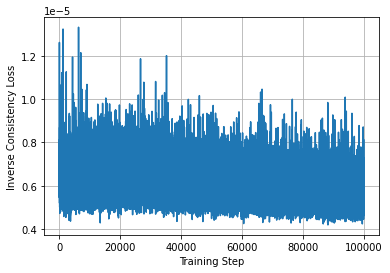
Learning maps between data samples is fundamental. Applications range from representation learning, image translation and generative modeling, to the estimation of spatial deformations. Such maps relate feature vectors, or map between feature spaces. Well-behaved maps should be regular, which can be imposed explicitly or may emanate from the data itself. We explore what induces regularity for spatial transformations, e.g., when computing image registrations. Classical optimization-based models compute maps between pairs of samples and rely on an appropriate regularizer for well-posedness. Recent deep learning approaches have attempted to avoid using such regularizers altogether by relying on the sample population instead. We explore if it is possible to obtain spatial regularity using an inverse consistency loss only and elucidate what explains map regularity in such a context. We find that deep networks combined with an inverse consistency loss and randomized off-grid interpolation yield well behaved, approximately diffeomorphic, spatial transformations. Despite the simplicity of this approach, our experiments present compelling evidence, on both synthetic and real data, that regular maps can be obtained without carefully tuned explicit regularizers, while achieving competitive registration performance.
翻译:数据样品之间的学习地图是最基本的。 应用范围从代表性学习、图像翻译和基因化模型到空间变形的估计等,这些地图涉及地貌矢量或地貌间间图。 守规的地图应该是定期的,可以明确强制使用,也可以由数据本身产生。 我们探索了空间变迁的规律性,例如,在计算图像登记时,如何引起空间变迁的规律性。 典型的优化模型在样本之间计算地图,并依靠适当的定序器进行保质。 最近的深层学习方法试图避免使用这种正规化器,而是依靠抽样人口来完全使用。 我们探索,如果有可能使用反一致性损失来获得空间常态性,并阐明在这种背景下解释地图常态性的原因。 我们发现,深层网络加上逆一致性损失和随机离网间插座的内插图产生良好的表现,大约是二变形空间变。 尽管这一方法十分简单,但我们在合成和真实数据上提出的令人信服的实验证据是,不需仔细调整清晰的固定地图,同时实现竞争性的登记。