The Price of Majority Support

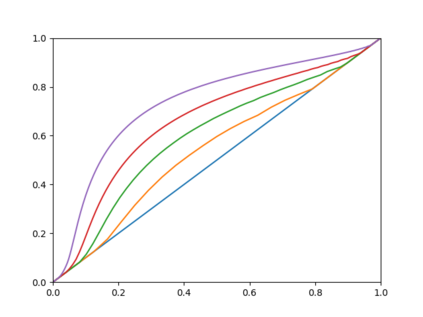
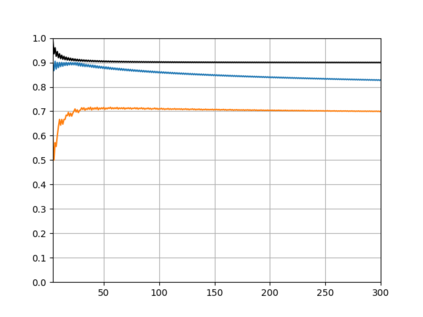
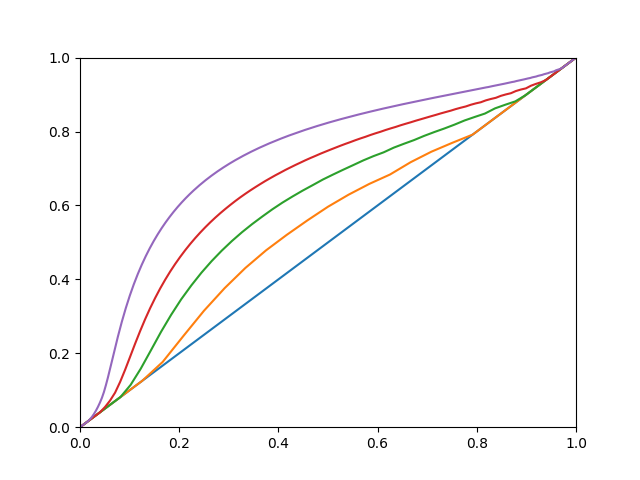
We consider the problem of finding a compromise between the opinions of a group of individuals on a number of mutually independent, binary topics. In this paper, we quantify the loss in representativeness that results from requiring the outcome to have majority support, in other words, the "price of majority support". Each individual is assumed to support an outcome if they agree with the outcome on at least as many topics as they disagree on. Our results can also be seen as quantifying Anscombes paradox which states that topic-wise majority outcome may not be supported by a majority. To measure the representativeness of an outcome, we consider two metrics. First, we look for an outcome that agrees with a majority on as many topics as possible. We prove that the maximum number such that there is guaranteed to exist an outcome that agrees with a majority on this number of topics and has majority support, equals $\ceil{(t+1)/2}$ where $t$ is the total number of topics. Second, we count the number of times a voter opinion on a topic matches the outcome on that topic. The goal is to find the outcome with majority support with the largest number of matches. We consider the ratio between this number and the number of matches of the overall best outcome which may not have majority support. We try to find the maximum ratio such that an outcome with majority support and this ratio of matches compared to the overall best is guaranteed to exist. For 3 topics, we show this ratio to be $5/6\approx 0.83$. In general, we prove an upper bound that comes arbitrarily close to $2\sqrt{6}-4\approx 0.90$ as $t$ tends to infinity. Furthermore, we numerically compute a better upper and a non-matching lower bound in the relevant range for $t$.