Robust Model Selection of Non Tree-Structured Gaussian Graphical Models

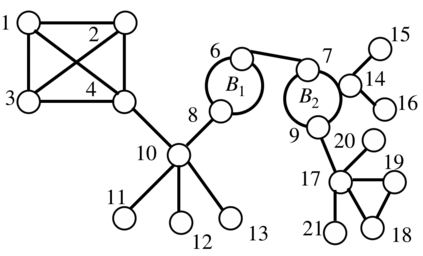
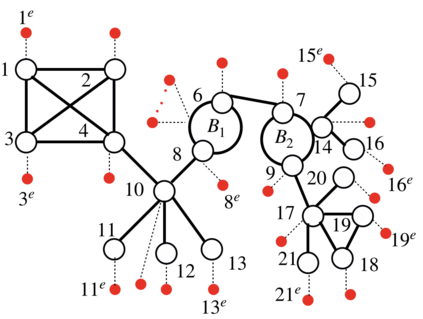
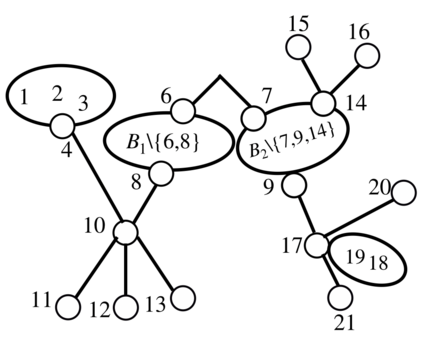
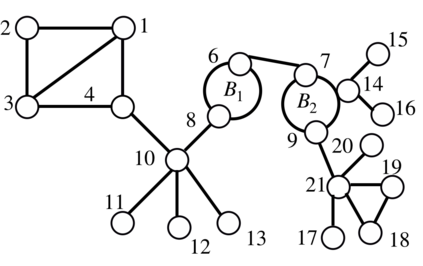
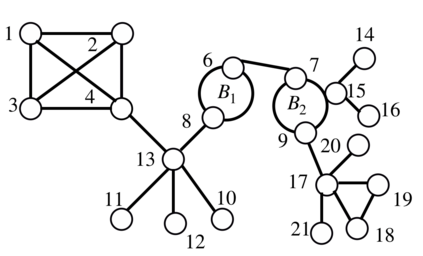
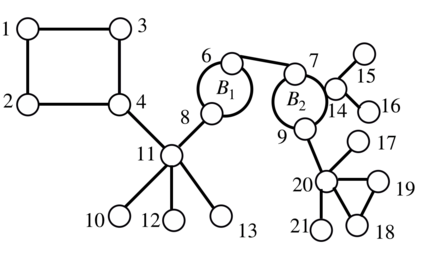
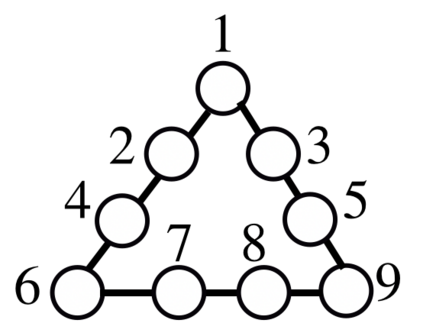
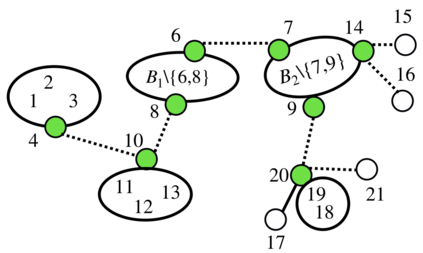
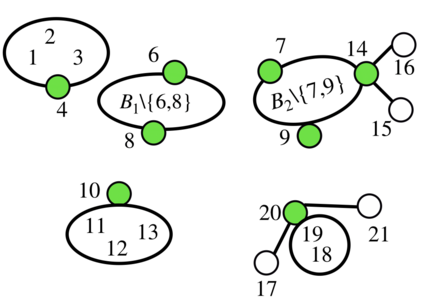
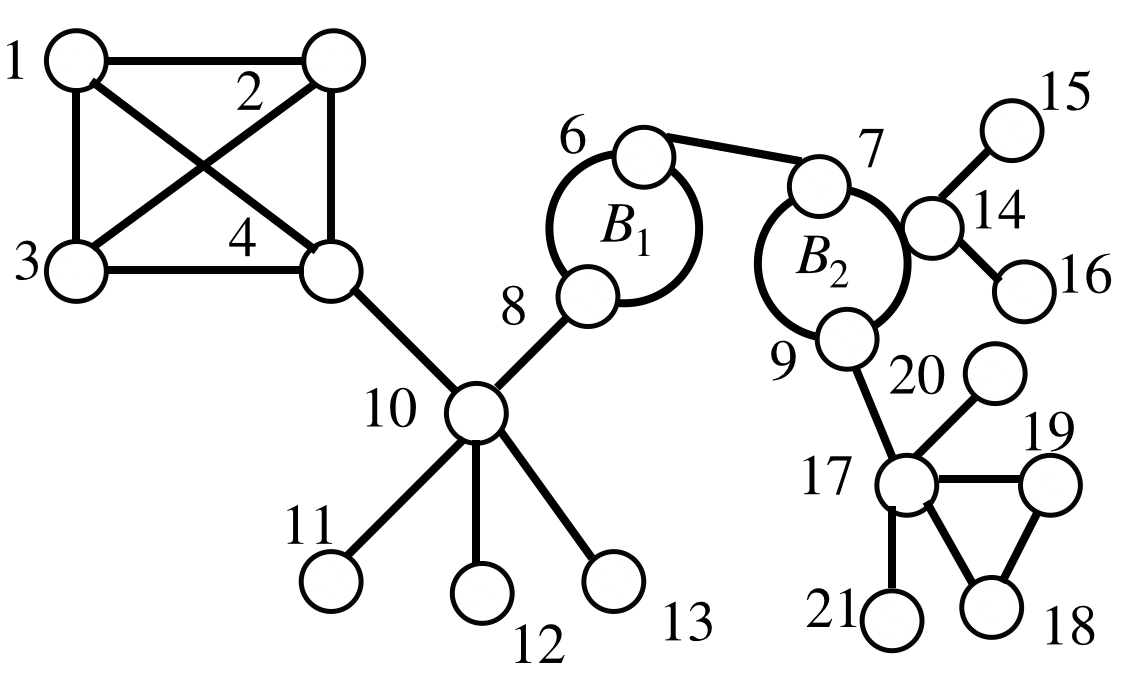
We consider the problem of learning the structure underlying a Gaussian graphical model when the variables (or subsets thereof) are corrupted by independent noise. A recent line of work establishes that even for tree-structured graphical models, only partial structure recovery is possible and goes on to devise algorithms to identify the structure up to an (unavoidable) equivalence class of trees. We extend these results beyond trees and consider the model selection problem under noise for non tree-structured graphs, as tree graphs cannot model several real-world scenarios. Although unidentifiable, we show that, like the tree-structured graphs, the ambiguity is limited to an equivalence class. This limited ambiguity can help provide meaningful clustering information (even with noise), which is helpful in computer and social networks, protein-protein interaction networks, and power networks. Furthermore, we devise an algorithm based on a novel ancestral testing method for recovering the equivalence class. We complement these results with finite sample guarantees for the algorithm in the high-dimensional regime.