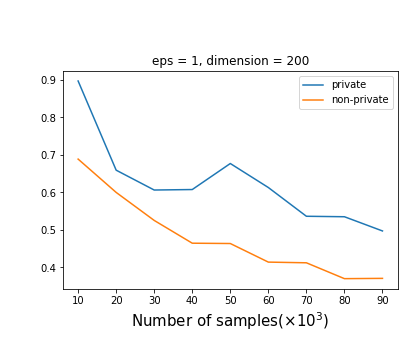
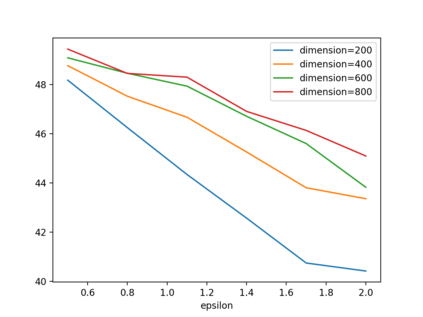
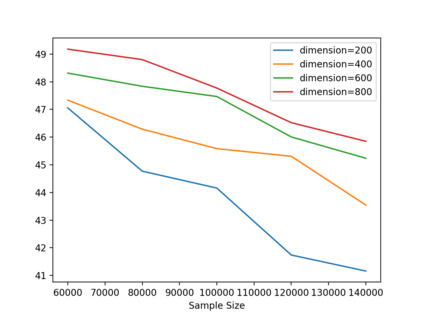
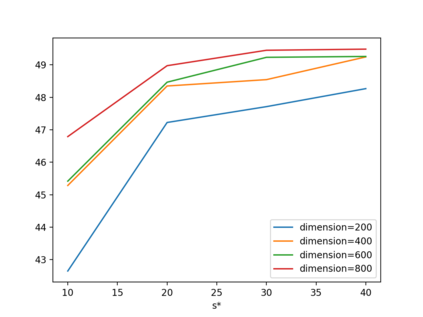
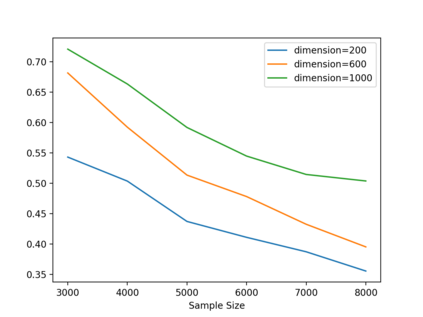
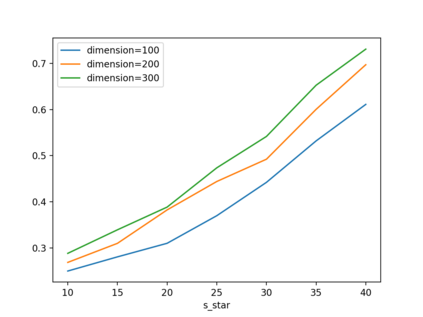
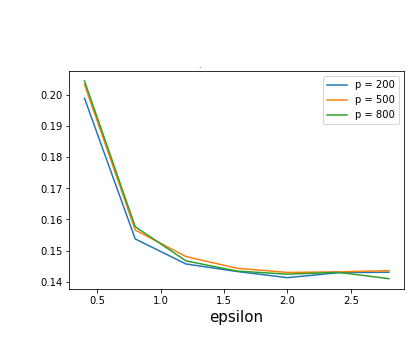
As one of the most fundamental problems in machine learning, statistics and differential privacy, Differentially Private Stochastic Convex Optimization (DP-SCO) has been extensively studied in recent years. However, most of the previous work can only handle either regular data distribution or irregular data in the low dimensional space case. To better understand the challenges arising from irregular data distribution, in this paper we provide the first study on the problem of DP-SCO with heavy-tailed data in the high dimensional space. In the first part we focus on the problem over some polytope constraint (such as the $\ell_1$-norm ball). We show that if the loss function is smooth and its gradient has bounded second order moment, it is possible to get a (high probability) error bound (excess population risk) of $\tilde{O}(\frac{\log d}{(n\epsilon)^\frac{1}{3}})$ in the $\epsilon$-DP model, where $n$ is the sample size and $d$ is the dimensionality of the underlying space. Next, for LASSO, if the data distribution that has bounded fourth-order moments, we improve the bound to $\tilde{O}(\frac{\log d}{(n\epsilon)^\frac{2}{5}})$ in the $(\epsilon, \delta)$-DP model. In the second part of the paper, we study sparse learning with heavy-tailed data. We first revisit the sparse linear model and propose a truncated DP-IHT method whose output could achieve an error of $\tilde{O}(\frac{s^{*2}\log d}{n\epsilon})$, where $s^*$ is the sparsity of the underlying parameter. Then we study a more general problem over the sparsity ({\em i.e.,} $\ell_0$-norm) constraint, and show that it is possible to achieve an error of $\tilde{O}(\frac{s^{*\frac{3}{2}}\log d}{n\epsilon})$, which is also near optimal up to a factor of $\tilde{O}{(\sqrt{s^*})}$, if the loss function is smooth and strongly convex.
翻译:作为机器学习、统计和差异隐私方面最根本的问题之一, 最近几年里已经广泛研究了“ 私自Stochastistic Constic $% 优化 ” (DP- SCO) 。 但是, 大多数先前的工作只能在低维空间案例中处理常规数据分发或非正常数据。 为了更好地了解数据分配不规则引起的挑战, 在本文件中, 我们提供了对高维空间中重尾数据问题的第一个研究。 在第一部分, 以美元为样本大小和美元为基底空间的维度, 以美元为基底值。 下一步, 以美元为基底值的数据流( 的可能性) 包绑( 超概率) (人口风险) dtilde{( 范围) (n\\ cilslon) 数据折叠成基数( =美元) 模型中, 以美元为基底值的基值和基底空间的维度( 美元) 。