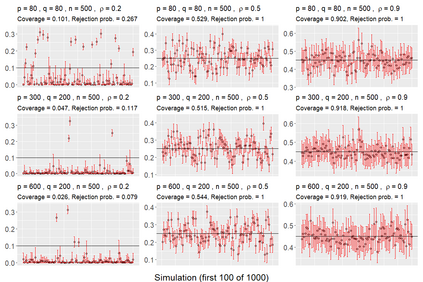
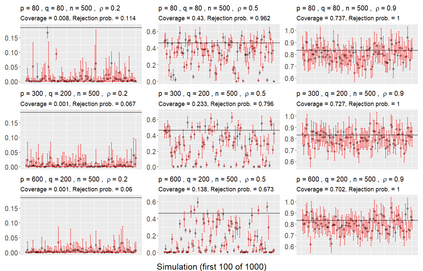
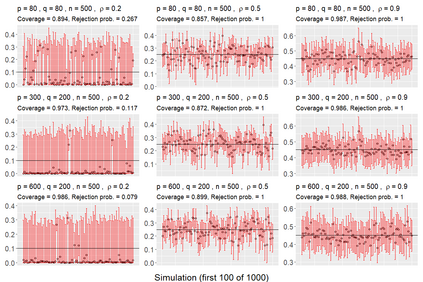
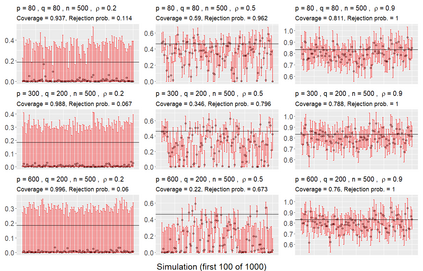
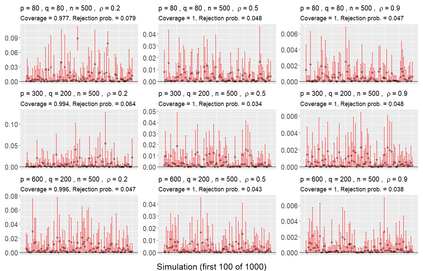
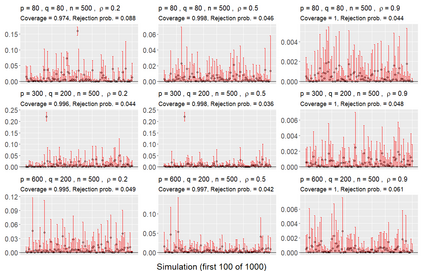
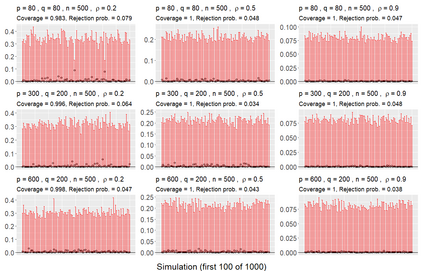
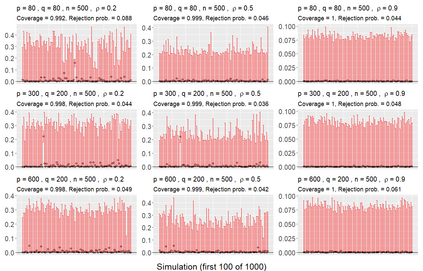
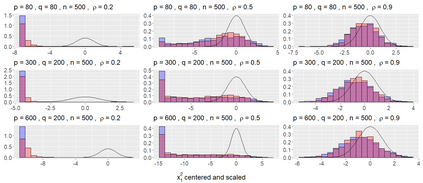
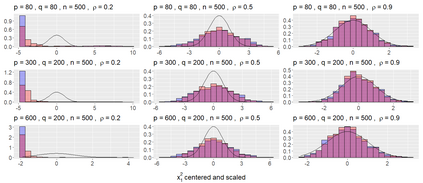
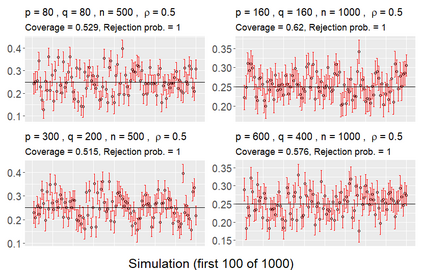
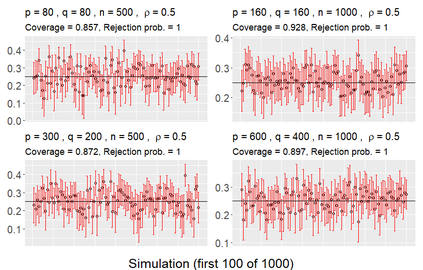
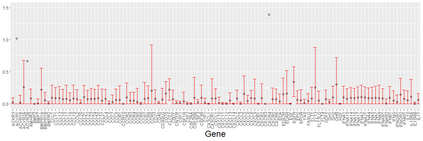
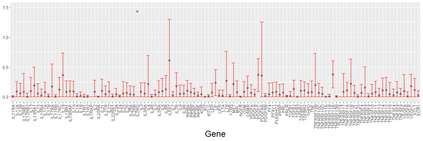
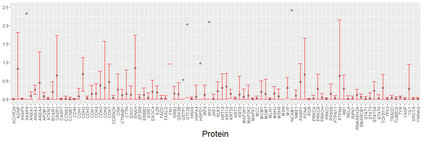
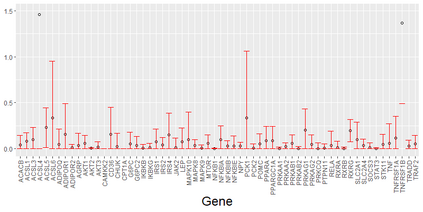
We consider asymptotically exact inference on the leading canonical correlation directions and strengths between two high dimensional vectors under sparsity restrictions. In this regard, our main contribution is the development of a loss function, based on which, one can operationalize a one-step bias-correction on reasonable initial estimators. Our analytic results in this regard are adaptive over suitable structural restrictions of the high dimensional nuisance parameters, which, in this set-up, correspond to the covariance matrices of the variables of interest. We further supplement the theoretical guarantees behind our procedures with extensive numerical studies.
翻译:我们认为,在宽度限制下,对两种高维矢量之间主要的能量性关联方向和强项的精确推断是站不住脚的,在这方面,我们的主要贡献是发展一种损失函数,在此基础上,我们可以对合理的初始估计器进行一步骤的偏差纠正,我们在这方面的分析结果是适应高维扰动参数的适当结构限制,在这一结构中,这些参数与相关变量的共变量矩阵相对应。我们进一步用广泛的数字研究来补充我们程序背后的理论保障。
相关内容
- Today (iOS and OS X): widgets for the Today view of Notification Center
- Share (iOS and OS X): post content to web services or share content with others
- Actions (iOS and OS X): app extensions to view or manipulate inside another app
- Photo Editing (iOS): edit a photo or video in Apple's Photos app with extensions from a third-party apps
- Finder Sync (OS X): remote file storage in the Finder with support for Finder content annotation
- Storage Provider (iOS): an interface between files inside an app and other apps on a user's device
- Custom Keyboard (iOS): system-wide alternative keyboards
Source: iOS 8 Extensions: Apple’s Plan for a Powerful App Ecosystem