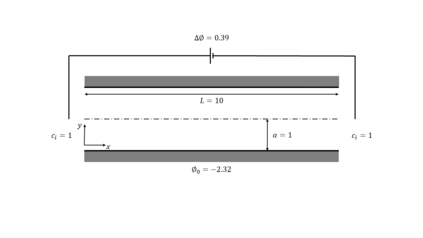
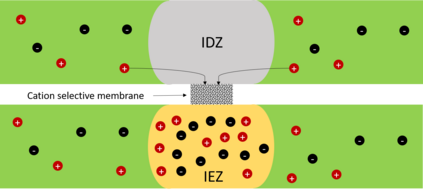
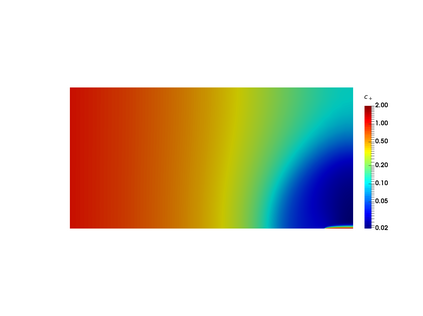
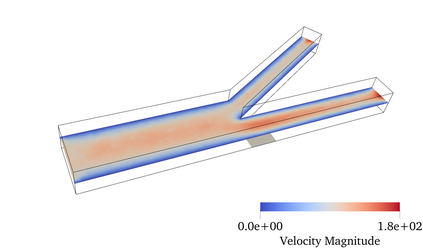
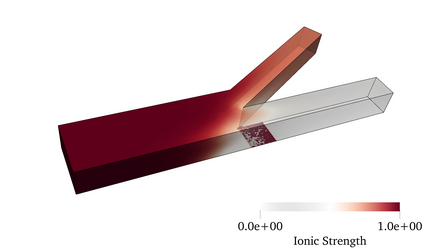
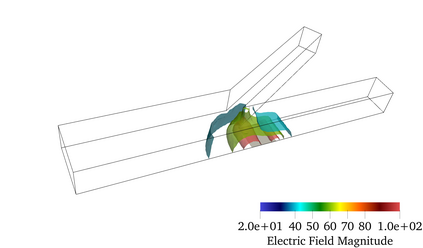
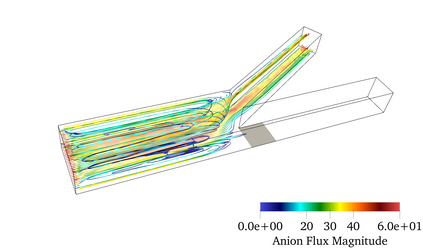
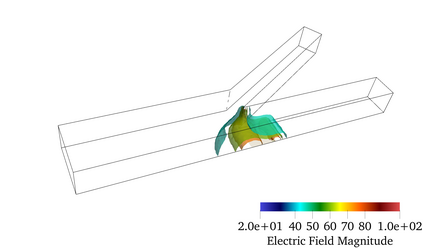
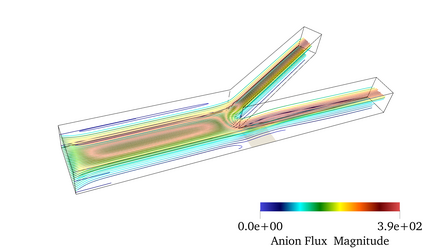
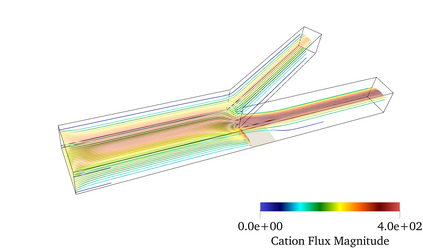
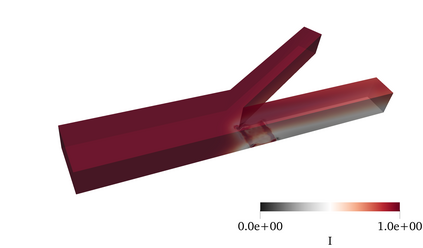
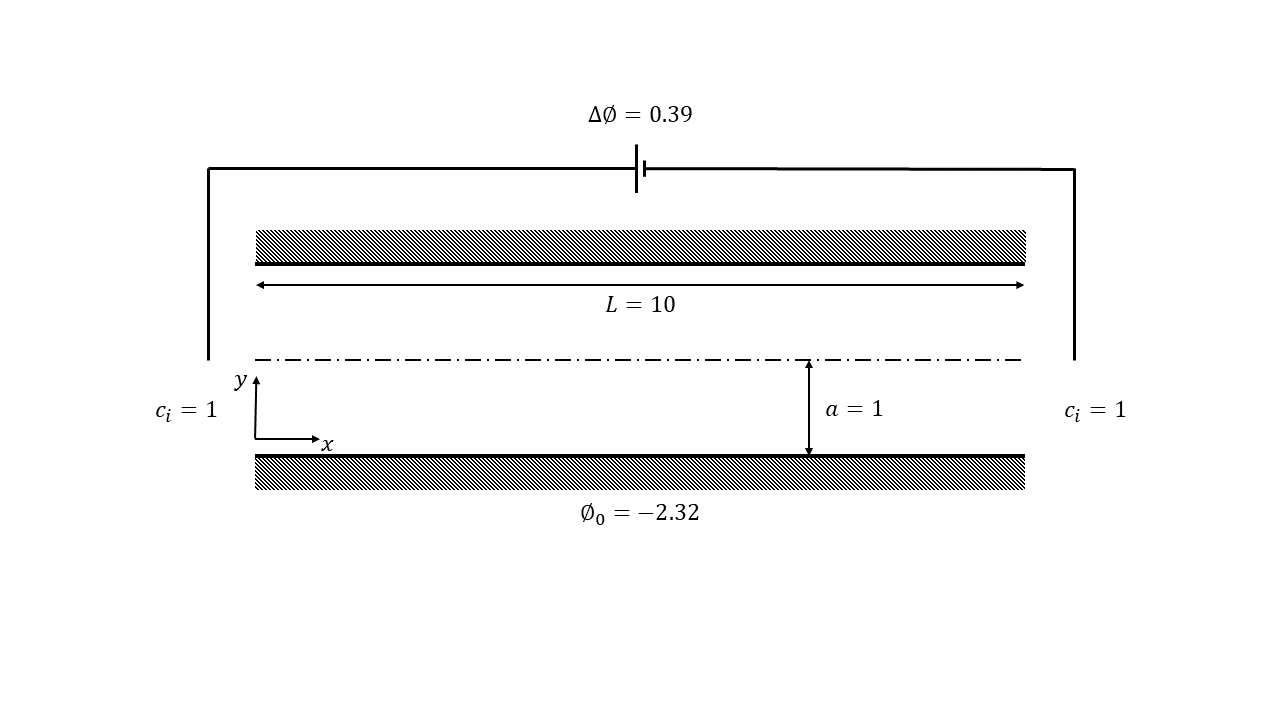
Finite element modeling of charged species transport has enabled analysis, design, and optimization of a diverse array of electrochemical and electrokinetic devices. These systems are represented by the Poisson-Nernst-Planck equations coupled with the Navier-Stokes equation, with a key quantity of interest being the current at the system boundaries. Accurately computing the current flux is challenging due to the small critical dimension of the boundary layers (small Debye layer) that require fine mesh resolution at the boundaries. We resolve this challenge by using the Dirichlet-to-Neumanntransformation to weakly impose the Dirichlet conditions for the Poisson-Nernst-Planck equations. The results obtained with weakly imposed Dirichlet boundary conditions showed excellent agreement with those obtained when conventional boundary conditions with highly resolved mesh we reemployed. Furthermore, the calculated current flux showed faster mesh convergence using weakly imposed conditions compared to the conventionally imposed Dirichlet boundary conditions. We illustrate the approach on canonical 3D problems that otherwise would have been computationally intractable to solve accurately. This approach substantially reduces the computational cost of model-ing electrochemical systems.
翻译:电动电化学和电动电动装置等离子体的微小临界层面(小型Debye层)使得对电动物种运输进行精密的模型化分析、设计和优化成为了挑战。这些系统由Poisson-Nernst-Planck等方程式和Navier-Stokes等方程式代表,其中关键的利益是系统边界的当前。精确计算目前的通量具有挑战性,因为边界层(小型Debye层)的临界层面很小,需要在边界上进行精细的网格解。我们通过利用Drichlet-Neumann变异来解决这一挑战,弱化地将Poisson-Nernst-Planck等方程式的 Dirichlet条件强加给Drichlet。以弱力加固的Drichlet边界条件获得的结果与当传统边界条件和我们重新使用高度溶解的网格线时获得的结果十分一致。此外,计算目前的通量显示,使用较弱的强加条件和传统Drichlet边界条件比传统强加的D边界条件更快地混合。我们计算得难以精确解的3D问题的方法说明。这个方法大大降低了了模型化学系统的计算成本。