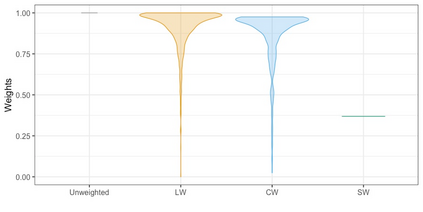
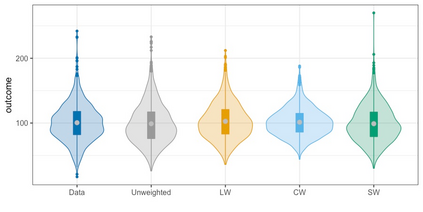
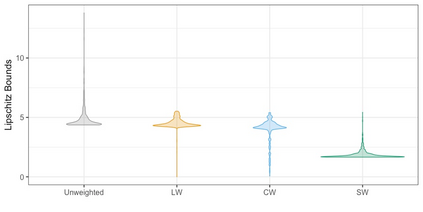
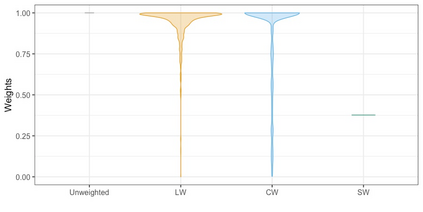
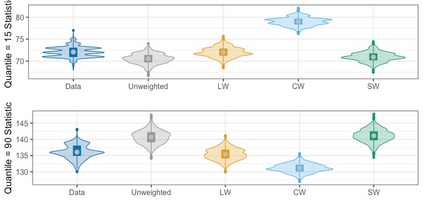
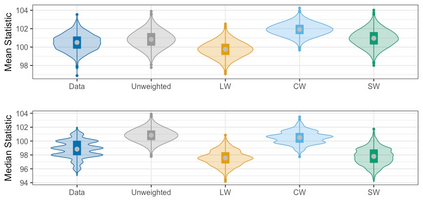
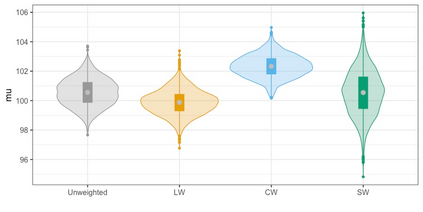
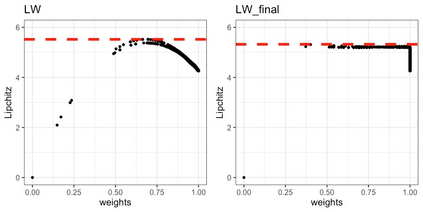
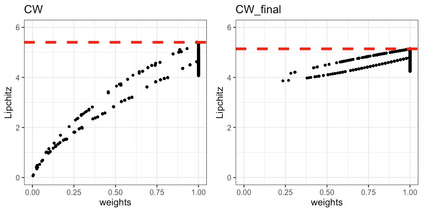
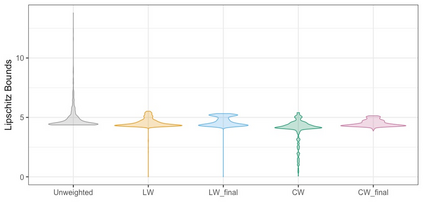
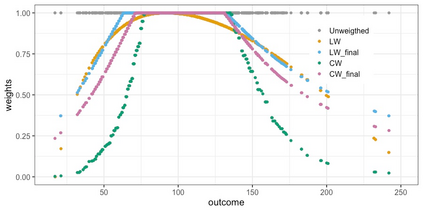
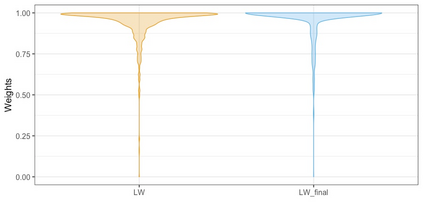
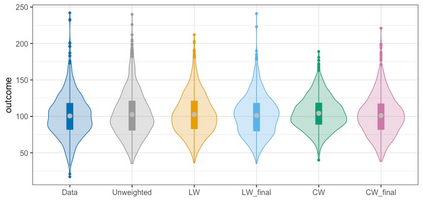
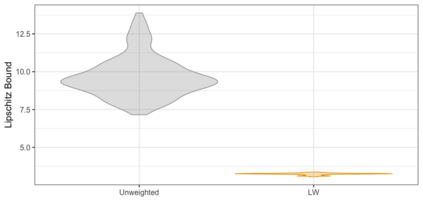
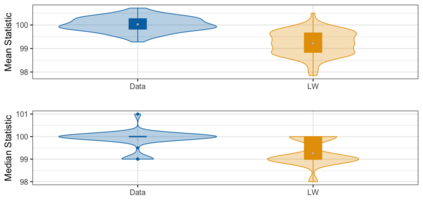
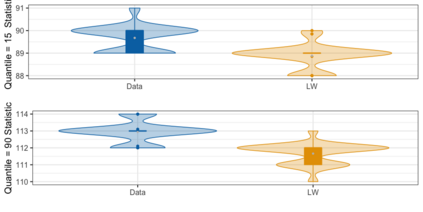
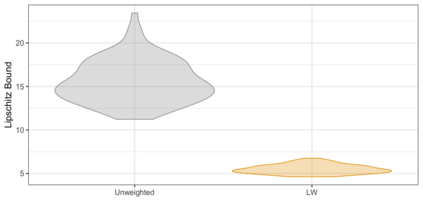
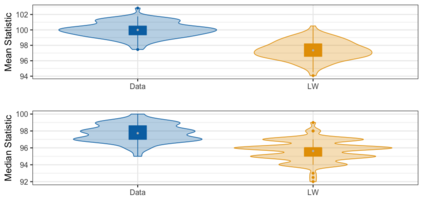
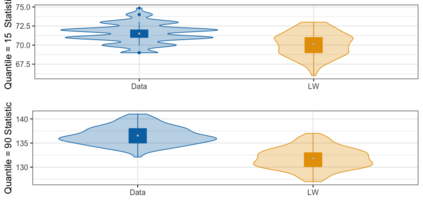
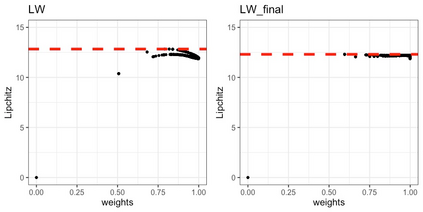
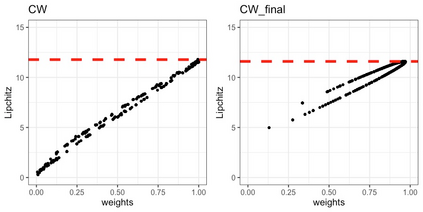
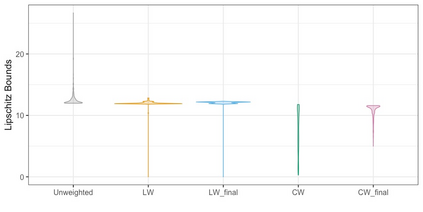
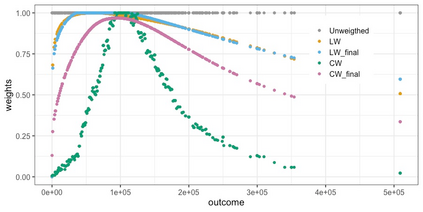
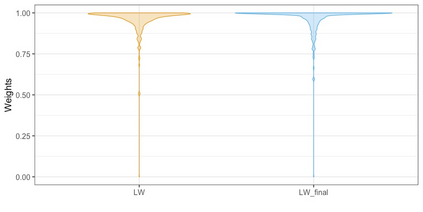
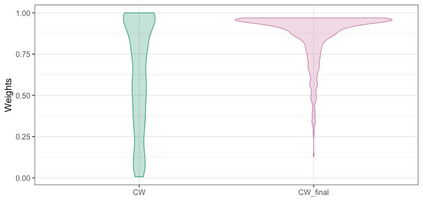
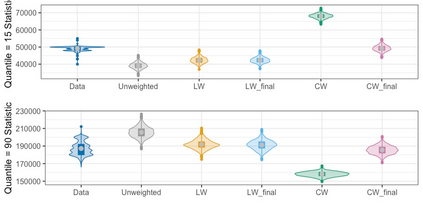
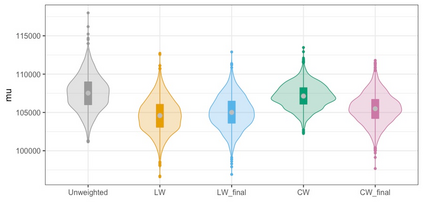
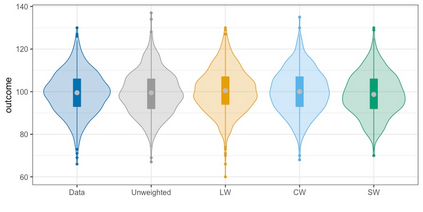
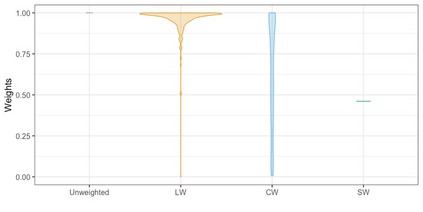
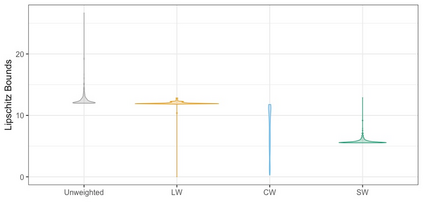
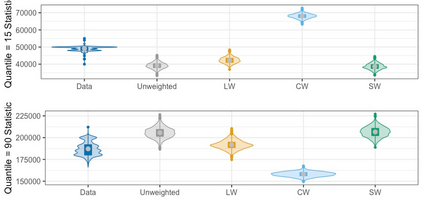
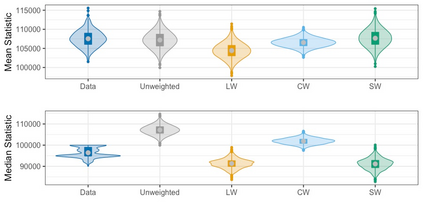
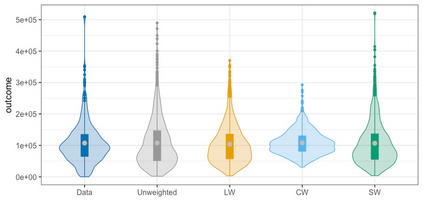
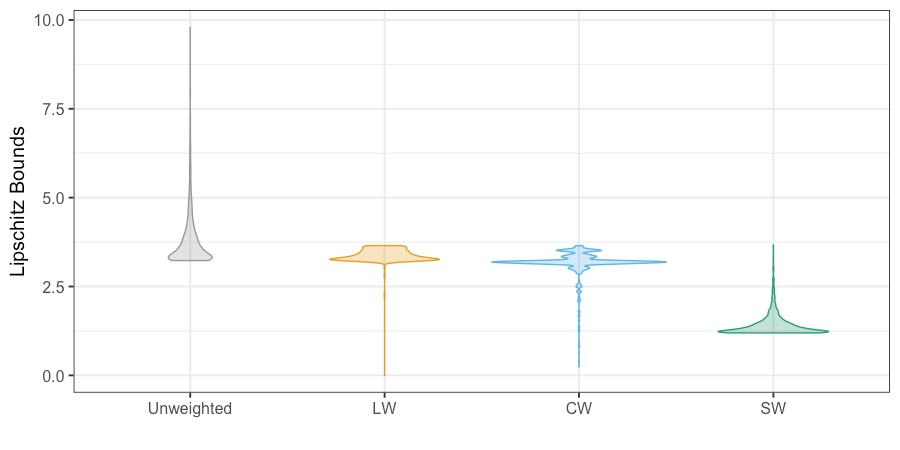
We present practical aspects of implementing a pseudo posterior synthesizer for microdata dissemination under a new re-weighting strategy for utility maximization. Our re-weighting strategy applies to any vector-weighting approach under which a vector of observation-indexed weight are used to downweight likelihood contributions for high disclosure risk records. We demonstrate our method on two different vector-weighted schemes that target high-risk records by exponentiating each of their likelihood contributions with a record-indexed weight, $\alpha_i \in [0,1]$ for record $i \in (1,\ldots,n)$. We compute the overall Lipschitz bound, $\Delta_{\bm{\alpha},\mathbf{x}}$, for the database $\mathbf{x}$, under each vector-weighted scheme where a local $\epsilon_{x} = 2\Delta_{\bm{\alpha},\mathbf{x}}$. Our new method for constructing record-indexed downeighting maximizes the data utility under any privacy budget for the vector-weighted synthesizers by adjusting the by-record weights, $(\alpha_{i})_{i = 1}^{n}$, such that their individual Lipschitz bounds, $\Delta_{\bm{\alpha},x_{i}}$, approach the bound for the entire database, $\Delta_{\bm{\alpha},\mathbf{x}}$. We illustrate our methods using simulated count data with and without over-dispersion-induced skewness and compare the results to a scalar-weighted synthesizer under the Exponential Mechanism (EM). We demonstrate our pDP result in a simulation study and our methods on a sample of the Survey of Doctorate Recipients.
翻译:我们展示了两种不同的矢量加权计划的方法,即以创纪录的重量计其可能贡献值, $\alpha_i\in [0,1,1,1,3,2,2,2,2,3,2,3,3,3,3,2,3,3,3,3,3,3,3,3,3,2,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,2,3,3,3,3,3,3,3,3,3,3,4,3,4,4,3,4,4,4,4,6,6,6,4,4,4,4,4,4,4,4,4,4,6,6,6,6,6,6,6,6,7,7,7,7,6,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,