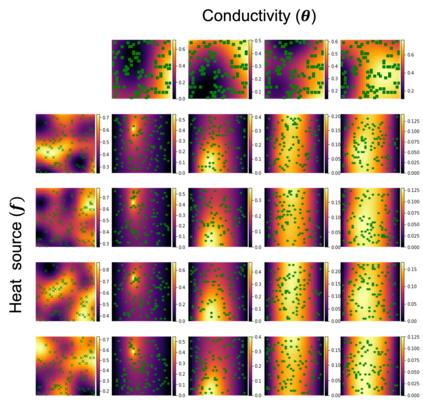
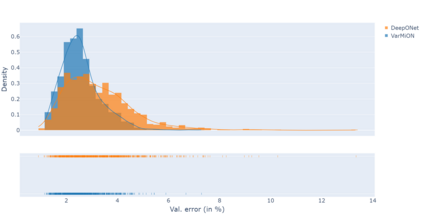
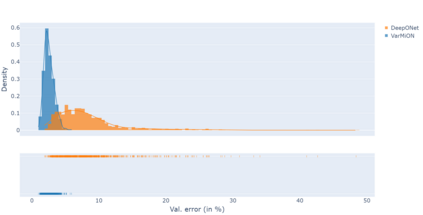
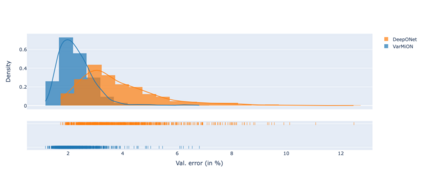
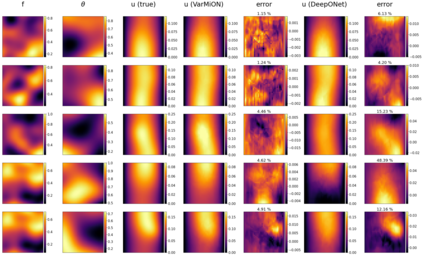
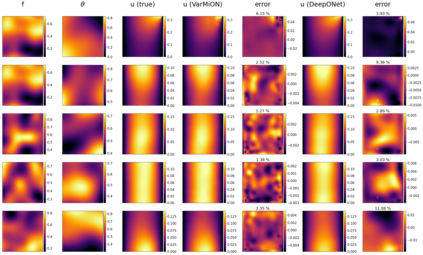
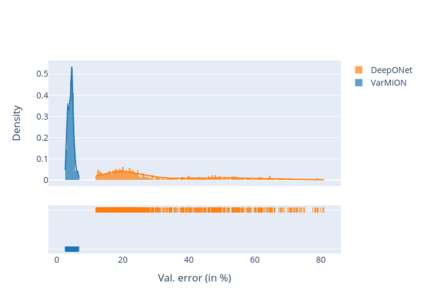
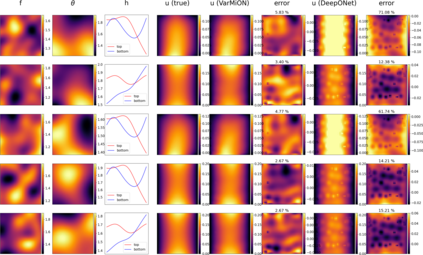
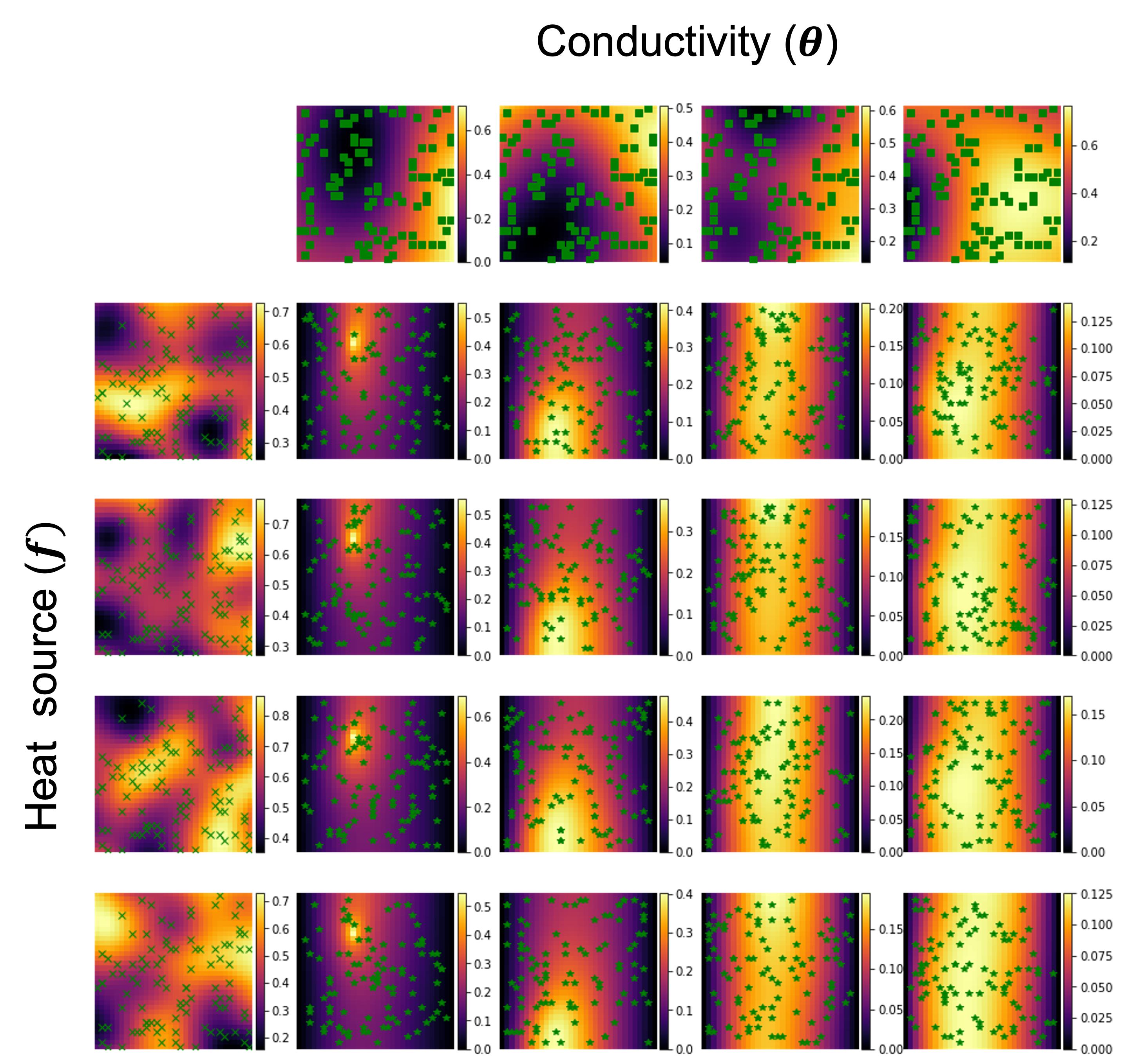
Operator networks have emerged as promising deep learning tools for approximating the solution to partial differential equations (PDEs). These networks map input functions that describe material properties, forcing functions and boundary data to the solution of a PDE. This work describes a new architecture for operator networks that mimics the form of the numerical solution obtained from an approximation of the variational or weak formulation of the problem. The application of these ideas to a generic elliptic PDE leads to a variationally mimetic operator network (VarMiON). Like the conventional Deep Operator Network (DeepONet) the VarMiON is also composed of a sub-network that constructs the basis functions for the output and another that constructs the coefficients for these basis functions. However, in contrast to the DeepONet, in the VarMiON the architecture of these networks is precisely determined. An analysis of the error in the VarMiON solution reveals that it contains contributions from the error in the training data, the training error, quadrature error in sampling input and output functions, and a "covering error" that measures the distance between the test input functions and the nearest functions in the training dataset. It also depends on the stability constants for the exact network and its VarMiON approximation. The application of the VarMiON to a canonical elliptic PDE reveals that for approximately the same number of network parameters, on average the VarMiON incurs smaller errors than a standard DeepONet. Further, its performance is more robust to variations in input functions, the techniques used to sample the input and output functions, the techniques used to construct the basis functions, and the number of input functions.
翻译:操作员网络已经出现,是接近部分差异方程式(PDE)解决方案的有希望的深层次学习工具。这些网络还绘制了描述物质属性、强制功能和边界数据以找到PDE的解决方案的子网络输入功能。这项工作描述了操作员网络的新结构,它模仿了从问题变异或微弱配方近似获得的数字解决方案的形式。将这些想法应用到通用的椭圆式 PDE 操作员网络(VarmiON) 中,这与传统的深操作员网络(DeepONet) 一样,它也由一个子网络组成,该子网络构建了输出的基值功能,为这些基值函数构建了基值。然而,与DeepON 相比,这些网络的构造准确确定了数字格式。对 VarmiON 解决方案的错误分析显示,它包含来自培训数据错误、培训错误、输入和输出功能的二次校正错误,以及“隐藏错误”,它用来测量 内输入的深度输入函数与最近输入函数之间的距离。它用于不断的 VarialMIL的运行数据,它也取决于常态数据的稳定性。它用来显示,它用来测量数据。