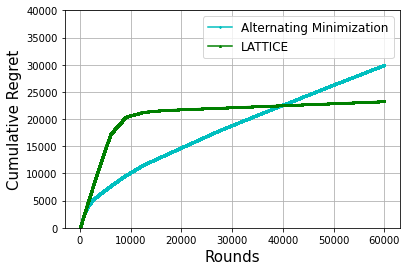
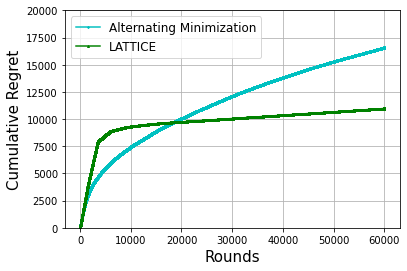
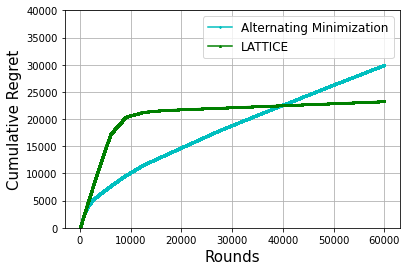
We consider the problem of latent bandits with cluster structure where there are multiple users, each with an associated multi-armed bandit problem. These users are grouped into \emph{latent} clusters such that the mean reward vectors of users within the same cluster are identical. At each round, a user, selected uniformly at random, pulls an arm and observes a corresponding noisy reward. The goal of the users is to maximize their cumulative rewards. This problem is central to practical recommendation systems and has received wide attention of late \cite{gentile2014online, maillard2014latent}. Now, if each user acts independently, then they would have to explore each arm independently and a regret of $\Omega(\sqrt{\mathsf{MNT}})$ is unavoidable, where $\mathsf{M}, \mathsf{N}$ are the number of arms and users, respectively. Instead, we propose LATTICE (Latent bAndiTs via maTrIx ComplEtion) which allows exploitation of the latent cluster structure to provide the minimax optimal regret of $\widetilde{O}(\sqrt{(\mathsf{M}+\mathsf{N})\mathsf{T}})$, when the number of clusters is $\widetilde{O}(1)$. This is the first algorithm to guarantee such a strong regret bound. LATTICE is based on a careful exploitation of arm information within a cluster while simultaneously clustering users. Furthermore, it is computationally efficient and requires only $O(\log{\mathsf{T}})$ calls to an offline matrix completion oracle across all $\mathsf{T}$ rounds.
翻译:在有多个用户的组状结构中, 我们考虑潜伏土匪的问题, 每个用户都存在多组土匪问题。 现在, 如果每个用户独立行事, 那么这些用户将不得不独立探索每个手臂, 同一组内用户的平均奖赏矢量是相同的。 在每轮中, 一个统一随机选择的用户会拉动一个手臂, 并观察到相应的响亮的奖励。 用户的目标是最大限度地增加其累积的奖赏。 这个问题是实用建议系统的核心, 并且受到晚期建议系统的广泛关注 。 现在, 如果每个用户独立行事, 那么他们就必须独立地探索每个手臂 。 然后他们必须独立地探索每个手臂中的平均奖赏矢量 。 $\ qrthfsf{ M} 。 用户的目标是将武器和用户的数量分别最大化 。 相反, 我们提议LATICICE (通过 comlient b&ix complil complain) 来利用隐藏的组状群状结构, 以最优化的值 $mall\\ mex= a glasmax crows a fal; rude; rual destrate;