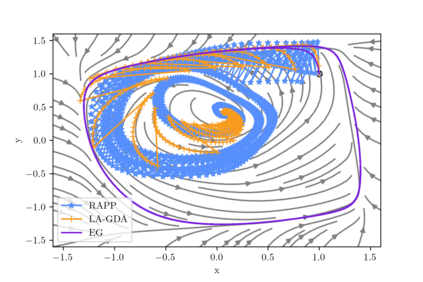
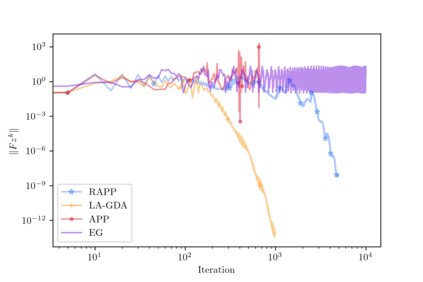
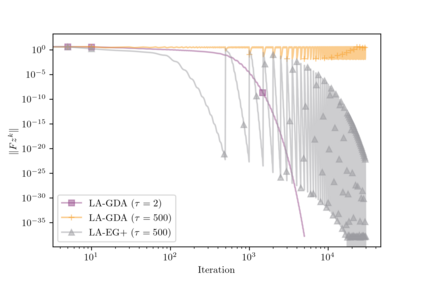
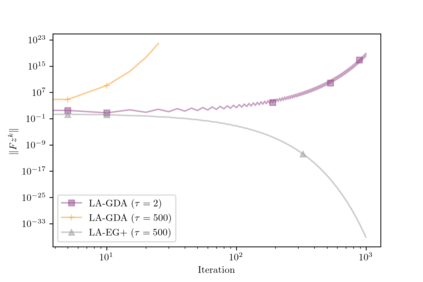
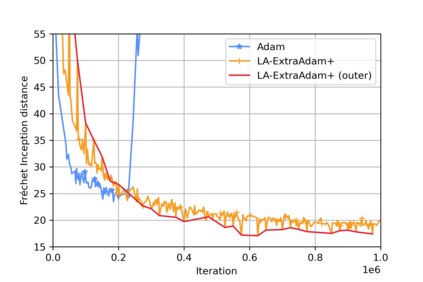
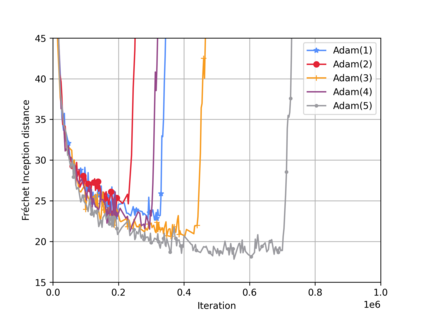
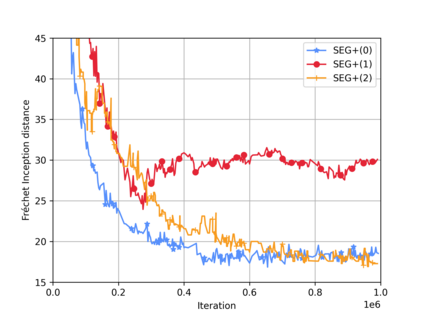
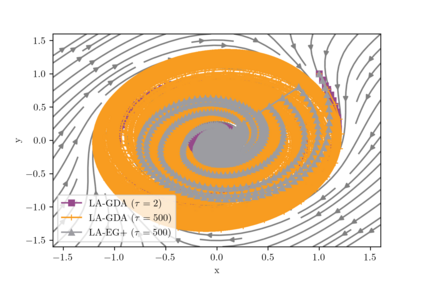
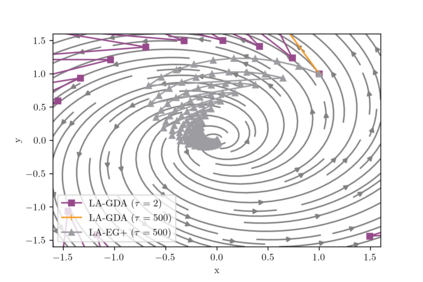
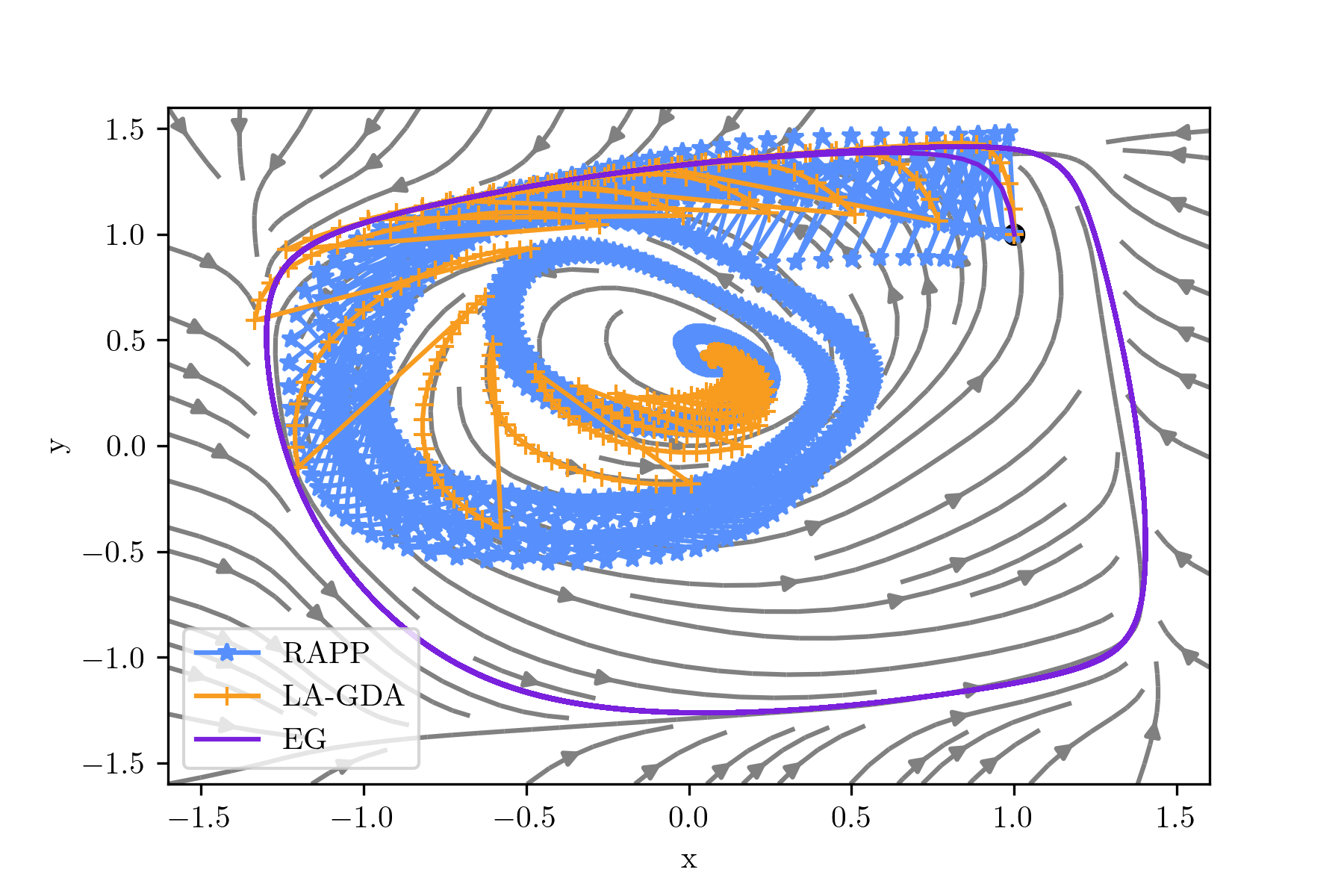
This paper presents a theoretical analysis of linear interpolation as a principled method for stabilizing (large-scale) neural network training. We argue that instabilities in the optimization process are often caused by the nonmonotonicity of the loss landscape and show how linear interpolation can help by leveraging the theory of nonexpansive operators. We construct a new optimization scheme called relaxed approximate proximal point (RAPP), which is the first 1-SCLI method to achieve last iterate convergence rates for $\rho$-comonotone problems while only requiring $\rho > -\tfrac{1}{2L}$. The construction extends to constrained and regularized settings. By replacing the inner optimizer in RAPP we rediscover the family of Lookahead algorithms for which we establish convergence in cohypomonotone problems even when the base optimizer is taken to be gradient descent ascent. The range of cohypomonotone problems in which Lookahead converges is further expanded by exploiting that Lookahead inherits the properties of the base optimizer. We corroborate the results with experiments on generative adversarial networks which demonstrates the benefits of the linear interpolation present in both RAPP and Lookahead.
翻译:暂无翻译