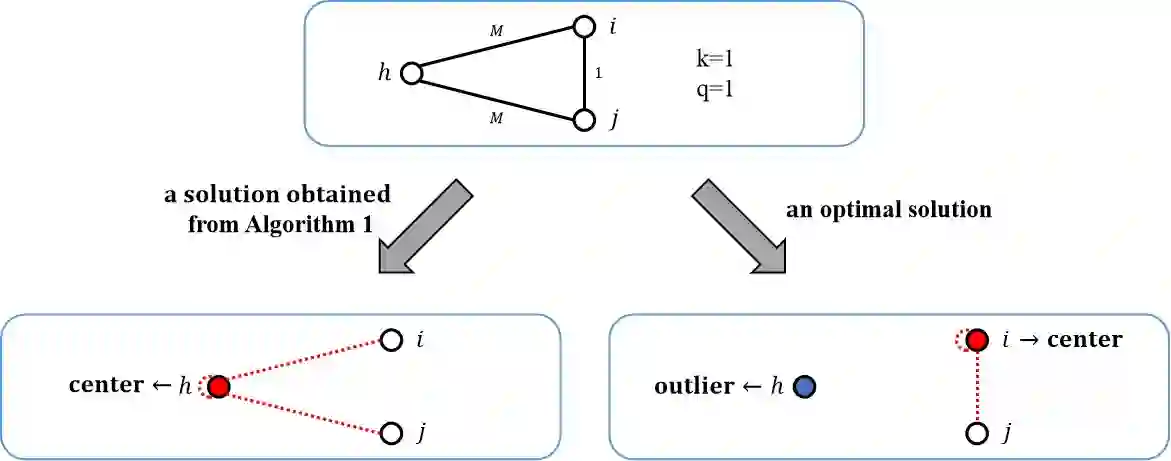
In this paper, we propose and investigate the individually fair $k$-center with outliers (IF$k$CO). In the IF$k$CO, we are given an $n$-sized vertex set in a metric space, as well as integers $k$ and $q$. At most $k$ vertices can be selected as the centers and at most $q$ vertices can be selected as the outliers. The centers are selected to serve all the not-an-outlier (i.e., served) vertices. The so-called individual fairness constraint restricts that every served vertex must have a selected center not too far way. More precisely, it is supposed that there exists at least one center among its $\lceil (n-q) / k \rceil$ closest neighbors for every served vertex. Because every center serves $(n-q) / k$ vertices on the average. The objective is to select centers and outliers, assign every served vertex to some center, so as to minimize the maximum fairness ratio over all served vertices, where the fairness ratio of a vertex is defined as the ratio between its distance with the assigned center and its distance with a $\lceil (n - q )/k \rceil_{\rm th}$ closest neighbor. As our main contribution, a 4-approximation algorithm is presented, based on which we develop an improved algorithm from a practical perspective.
翻译:在本文中, 我们提议并调查个人公平的 $k$ 中心与外部线( IF$k$ CO ) 。 在 IF$k$ CO 中, 我们得到了一个以美元为大小的顶点设置在一个公尺空间里, 以及整数美元和美元。 最多可以选择以美元为中心, 最多可以选择以美元为顶点, 最多可以选择以美元为外端。 中心被选中为所有非外端( 即, 已服务过) 的顶点服务。 所谓的个人公平限制限制了每个服务过的顶点必须有一个不远的选定中心。 更准确地说, 假设每个服务过的顶点至少有一个中心是作为中心, 每个顶点可以选择以美元为中心, 最多以美元为顶点。 目标是选择所有改进的中心和外端点, 将每个服务过的顶点指定为某个中心, 以最远处为中心, 以最远处为准, 。 其最高的顶端比例是 。