Anytime Optimal PSRO for Two-Player Zero-Sum Games

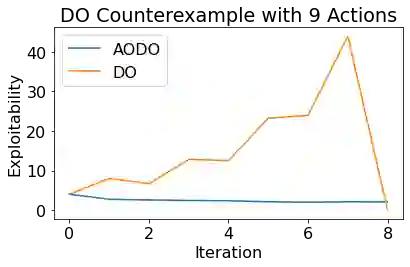
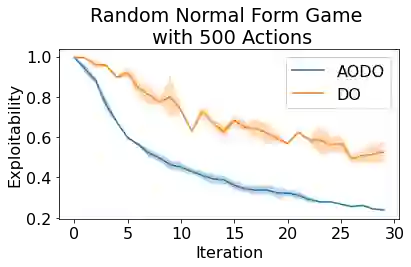
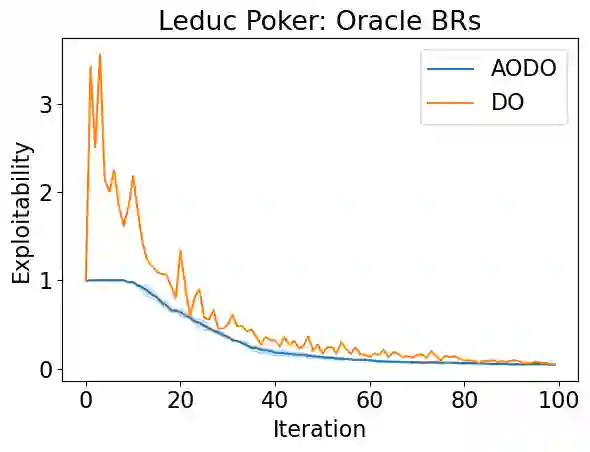
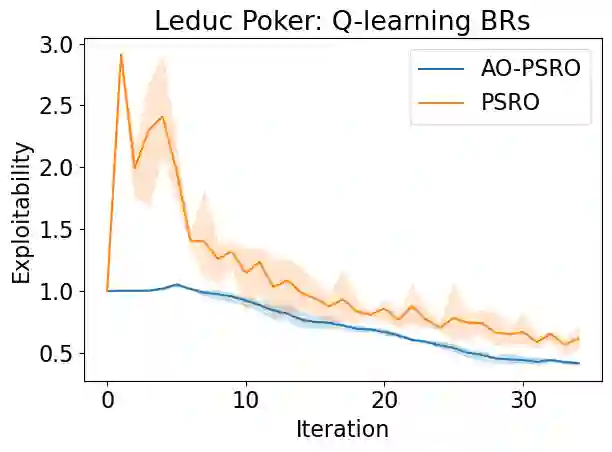
Policy Space Response Oracles (PSRO) is a multi-agent reinforcement learning algorithm for games that can handle continuous actions and has empirically found approximate Nash equilibria in large games. PSRO is based on the tabular Double Oracle (DO) method, an algorithm that is guaranteed to converge to a Nash equilibrium, but may increase exploitability from one iteration to the next. We propose Anytime Optimal Double Oracle (AODO), a tabular double oracle algorithm for 2-player zero-sum games that is guaranteed to converge to a Nash equilibrium while decreasing exploitability from iteration to iteration. Unlike DO, in which the meta-strategy is based on the restricted game formed by each player's strategy sets, AODO finds the meta-strategy for each player that minimizes its exploitability against any policy in the full, unrestricted game. We also propose a method of finding this meta-strategy via a no-regret algorithm updated against a continually-trained best response, called RM-BR DO. Finally, we propose Anytime Optimal PSRO, a version of AODO that calculates best responses via reinforcement learning. In experiments on Leduc poker and random normal form games, we show that our methods achieve far lower exploitability than DO and PSRO and never increase exploitability.