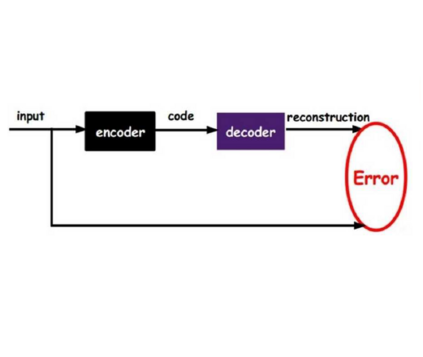
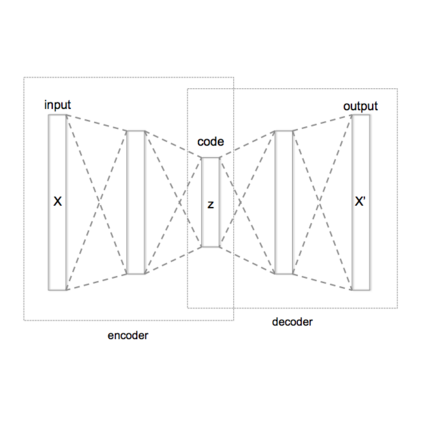
Variational autoencoders (VAEs) have recently been used for unsupervised disentanglement learning of complex density distributions. Numerous variants exist to encourage disentanglement in latent space while improving reconstruction. However, none have simultaneously managed the trade-off between attaining extremely low reconstruction error and a high disentanglement score. We present a generalized framework to handle this challenge under constrained optimization and demonstrate that it outperforms state-of-the-art existing models as regards disentanglement while balancing reconstruction. We introduce three controllable Lagrangian hyperparameters to control reconstruction loss, KL divergence loss and correlation measure. We prove that maximizing information in the reconstruction network is equivalent to information maximization during amortized inference under reasonable assumptions and constraint relaxation.
翻译:最近利用变化式自动电解码器(VAEs)在不受监督的情况下对复杂的密度分布进行分解学习。存在许多变异器,鼓励在改善重建的同时在潜在空间进行分解;然而,没有一种变异器同时处理在完成极低重建错误和高度分解得分之间的权衡。我们提出了一个普遍框架,以在有限的优化条件下应对这一挑战,并表明在平衡重建的同时分解比现有最先进的模式要好。我们引入了三种可控的拉格朗格超参数,以控制重建损失、KL差异损失和相关性计量。我们证明,在重建网络中最大限度地利用信息等同于在合理假设和制约放松下进行摊销性推断时的信息最大化。