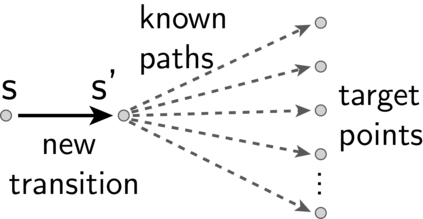
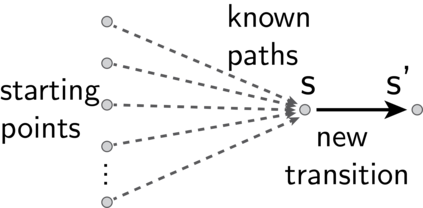
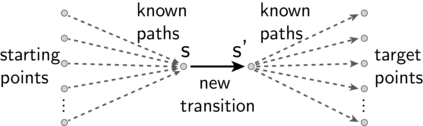
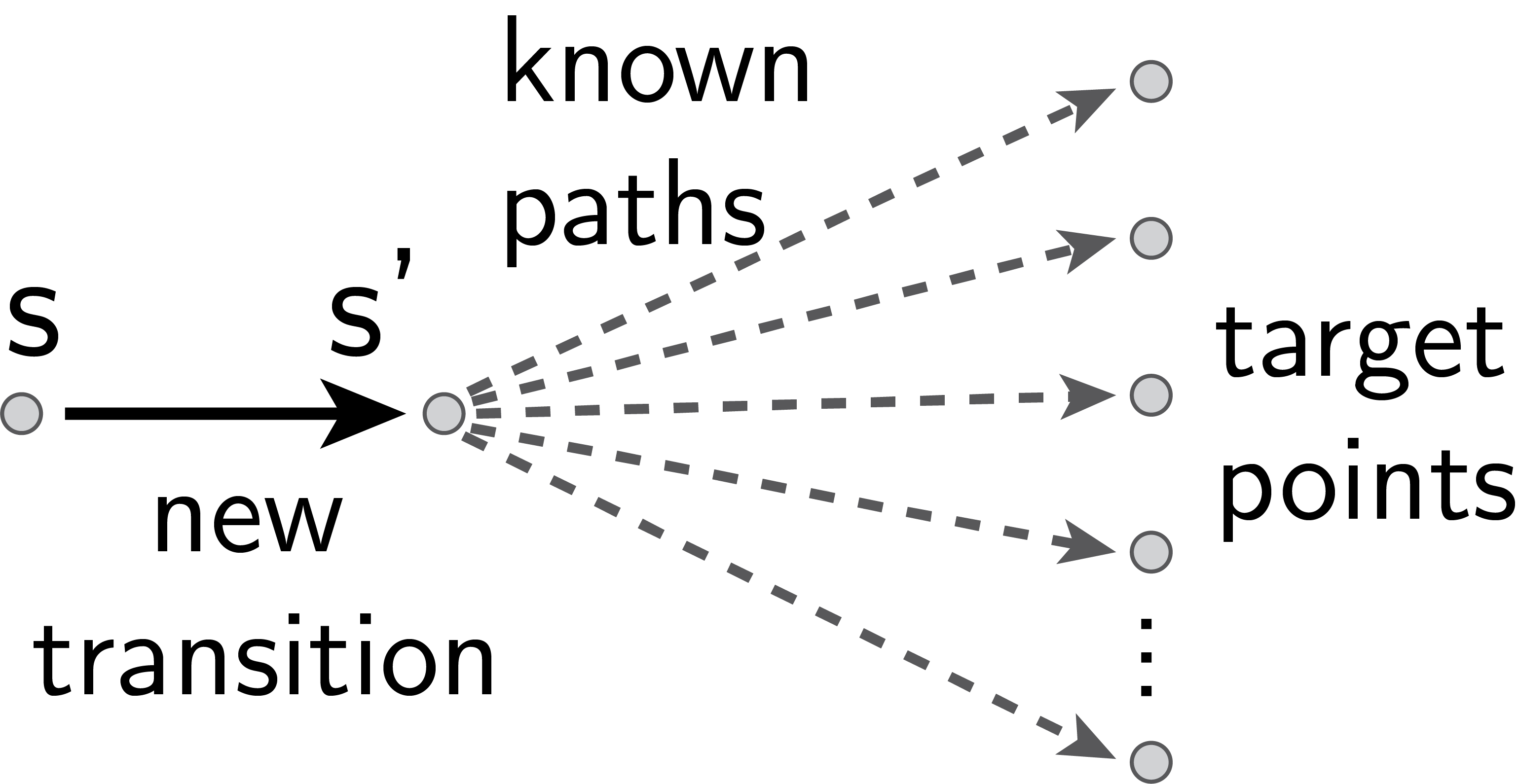
In reinforcement learning, temporal difference-based algorithms can be sample-inefficient: for instance, with sparse rewards, no learning occurs until a reward is observed. This can be remedied by learning richer objects, such as a model of the environment, or successor states. Successor states model the expected future state occupancy from any given state for a given policy and are related to goal-dependent value functions, which learn how to reach arbitrary states. We formally derive the temporal difference algorithm for successor state and goal-dependent value function learning, either for discrete or for continuous environments with function approximation. Especially, we provide finite-variance estimators even in continuous environments, where the reward for exactly reaching a goal state becomes infinitely sparse. Successor states satisfy more than just the Bellman equation: a backward Bellman operator and a Bellman-Newton (BN) operator encode path compositionality in the environment. The BN operator is akin to second-order gradient descent methods and provides the true update of the value function when acquiring more observations, with explicit tabular bounds. In the tabular case and with infinitesimal learning rates, mixing the usual and backward Bellman operators provably improves eigenvalues for asymptotic convergence, and the asymptotic convergence of the BN operator is provably better than TD, with a rate independent from the environment. However, the BN method is more complex and less robust to sampling noise. Finally, a forward-backward (FB) finite-rank parameterization of successor states enjoys reduced variance and improved samplability, provides a direct model of the value function, has fully understood fixed points corresponding to long-range dependencies, approximates the BN method, and provides two canonical representations of states as a byproduct.
翻译:在加固学习中,基于时间差异的算法可能缺乏抽样效率:例如,由于奖励少,在看到奖励之前不会进行学习。这可以通过学习环境模型或继承国等更丰富的对象来弥补,继承国为特定政策从任何特定状态来模拟预期的未来状态占用,并与基于目标的值函数相关,这些功能学会如何到达任意状态。我们正式为继承国和基于目标的值函数学习得出时间差异算法,无论是为离散还是为功能接近的连续环境学习。特别是,我们甚至在连续环境中提供有限差异的估测器,因为在那里,完全达到目标状态的奖赏会变得极其少。继承国不仅满足贝尔曼方程式:一个落后的贝尔曼操作员和一个贝尔曼-纽顿(BN)操作员在环境中将路径编码为路径。 BN操作员类似于次级梯度的梯度下降方法,在获得更多观测时提供真实的数值更新,以明确的表框值表示。在表格中,通过极小的学习速度,将通常的和落后的Bellman操作员的周期差率,而是将正常的比正常的周期更精确地改进了Brent速度,最终地改进了Bral-ration-rent-ration法,但更能提供更精确的精确的比更精确的比更精确地改进。