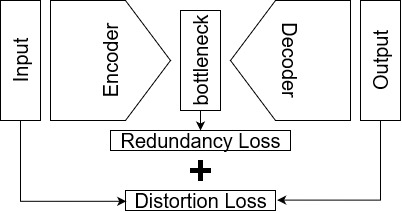
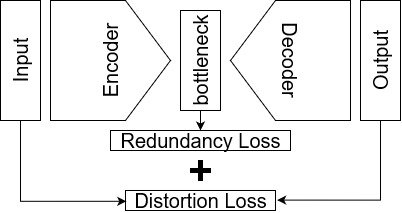
Autoencoders are a type of unsupervised neural networks, which can be used to solve various tasks, e.g., dimensionality reduction, image compression, and image denoising. An AE has two goals: (i) compress the original input to a low-dimensional space at the bottleneck of the network topology using an encoder, (ii) reconstruct the input from the representation at the bottleneck using a decoder. Both encoder and decoder are optimized jointly by minimizing a distortion-based loss which implicitly forces the model to keep only those variations of input data that are required to reconstruct the and to reduce redundancies. In this paper, we propose a scheme to explicitly penalize feature redundancies in the bottleneck representation. To this end, we propose an additional loss term, based on the pair-wise correlation of the neurons, which complements the standard reconstruction loss forcing the encoder to learn a more diverse and richer representation of the input. We tested our approach across different tasks: dimensionality reduction using three different dataset, image compression using the MNIST dataset, and image denoising using fashion MNIST. The experimental results show that the proposed loss leads consistently to superior performance compared to the standard AE loss.
翻译:自动电解码器是一种不受监督的神经网络,可用于解决各种任务,例如维度减少、图像压缩和图像拆卸等。一个 AE 有两个目标:(一) 使用编码器压缩原始输入到网络表层瓶颈的低维空间,(二) 使用解码器重建在瓶颈处的表示式输入。通过最大限度地减少基于扭曲的损失来优化编码器和解码器,这间接迫使模型只保留重建并减少冗余所需的输入数据的变化。在本文件中,我们提出了一个计划,明确惩罚瓶颈表层代表的冗余特征。为此,我们提议根据神经元的双向关系,增加一个损失期,以补充标准重建损失,迫使电解码器学习更多样化和更丰富的输入。我们测试了我们在不同任务中的做法:使用三个不同的数据设置来减少数据,使用MNMIST数据设置来压缩图像。我们建议采用高端数据设置来明确惩罚瓶颈表的重复性能,并用高端的图像显示测试结果。