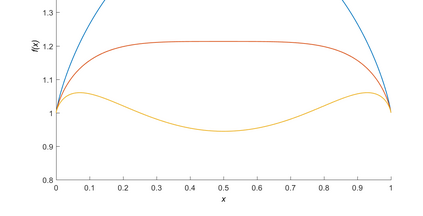
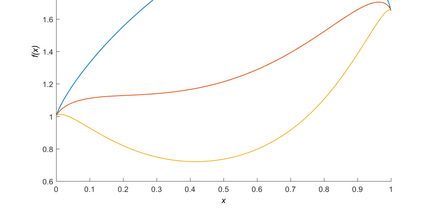
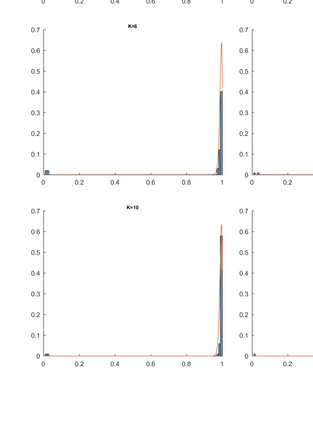
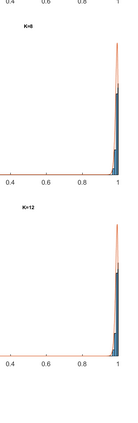
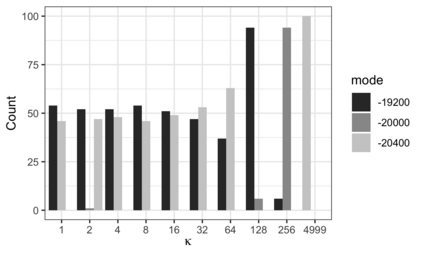
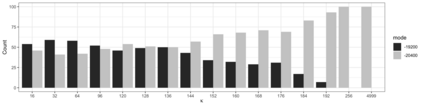
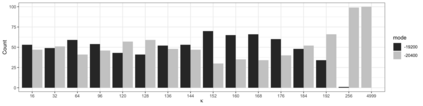
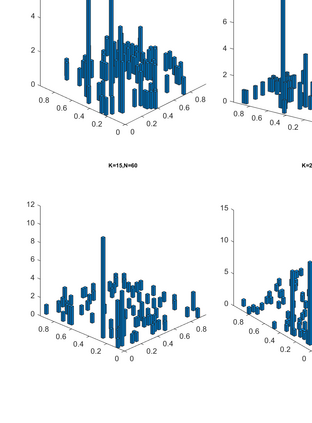
We consider nearest neighbor weighted random walks on the $d$-dimensional box $[n]^d$ that are governed by some function $g:[0,1] \ra [0,\iy)$, by which we mean that standing at $x$, a neighbor $y$ of $x$ is picked at random and the walk then moves there with probability $(1/2)g(n^{-1}y)/(g(n^{-1}y)+g(n^{-1}x))$. We do this for $g$ of the form $f^{m_n}$ for some function $f$ which assumed to be analytically well-behaved and where $m_n \ra \iy$ as $n \ra \iy$. This class of walks covers an abundance of interesting special cases, e.g., the mean-field Potts model, posterior collapsed Gibbs sampling for Latent Dirichlet allocation and certain Bayesian posteriors for models in nuclear physics. The following are among the results of this paper: \begin{itemize} \item If $f$ is unimodal with negative definite Hessian at its global maximum, then the mixing time of the random walk is $O(n\log n)$. \item If $f$ is multimodal, then the mixing time is exponential in $n$, but we show that there is a simulated annealing scheme governed by $f^K$ for an increasing sequence of $K$ that mixes in time $O(n^2)$. Using a varying step size that decreases with $K$, this can be taken down to $O(n\log n)$. \item If the process is studied on a general graph rather than the $d$-dimensional box, a simulated annealing scheme expressed in terms of conductances of the underlying network, works similarly. \end{itemize} Several examples are given, including the ones mentioned above.
翻译:我们认为最接近的邻居在美元维度框 $[n]+g(n}-1}x) 上随机行走。我们这样做的理由是以某种函数 $g 为单位的 美元 : [0] 1\ ra [0,\ iy] 美元, 我们的意思是, 以美元为单位, 随机挑选 $x美元, 以美元为单位, 然后行走方式移动到那里, 概率为$( 1/2)g( n ⁇ -1}y) /( g( n) +g( n ⁇ ) +g( n}) +g( n}) +( g) (n}-1}x) 美元 。 对于某种函数, 美元( g), 以美元为单位, 美元为单位, 假设是分析好的, 美元 美元 美元 美元, 美元 以美元 美元 美元 美元 。 这个行走方式的行走方式是 。