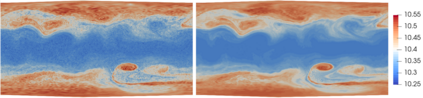
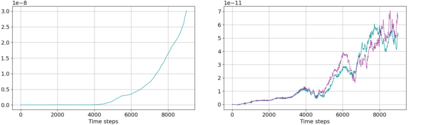
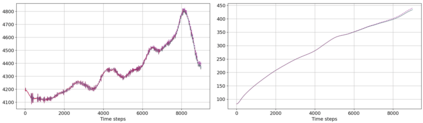
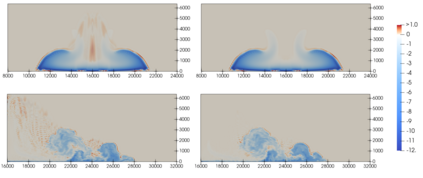
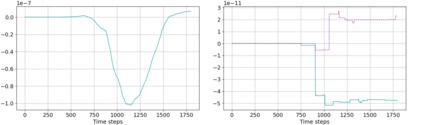
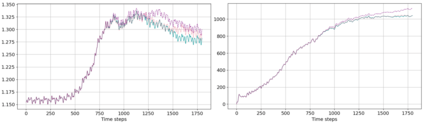
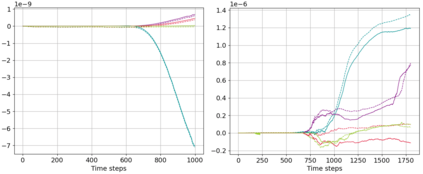
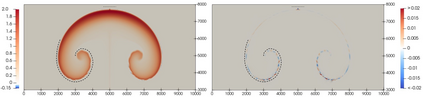
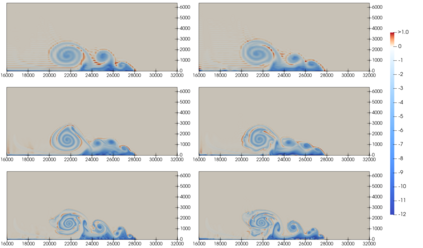
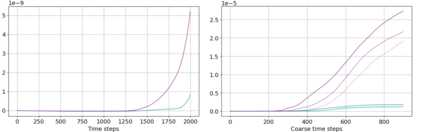
We present an energy conserving space discretisation based on a Poisson bracket that can be used to derive the dry compressible Euler as well as thermal shallow water equations. It is formulated using the compatible finite element method, and extends the incorporation of upwinding for the shallow water equations as described in Wimmer, Cotter, and Bauer (2019). While the former is restricted to DG upwinding, an energy conserving SUPG scheme for the (partially) continuous Galerkin thermal field space is newly introduced here. The energy conserving property is validated by coupling the Poisson bracket based spatial discretisation to an energy conserving time discretisation. Further, the discretisation is demonstrated to lead to an improved temperature field development with respect to stability when upwinding is included. An approximately energy conserving full discretisation with a smaller computational cost is also presented.
翻译:我们展示了一种基于 Poisson 括号的节能空间分解,可用于得出干压缩 Euler 和热浅水方程式,它使用兼容的有限元素法进行配制,并扩展了Wimmer、Cotter 和 Bauer (2019年) 所述浅水方程式的顺流整合,前者仅限于DG 顺流,而前者则在此新引入了(部分)连续的Galerkin热场空间的节能超液化计划。节能产权通过将基于Poisson 括号的空间分解与节能时间分解相结合而得到验证。此外,离化证明在包括上风时,离化有助于改善温度场的开发。还介绍了一种大约节能、计算成本较小的全分解的节能方案。