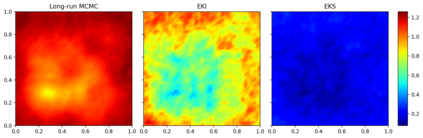
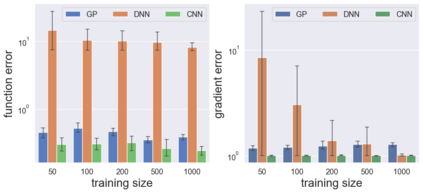
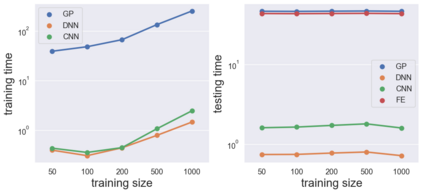
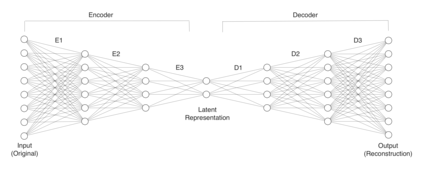
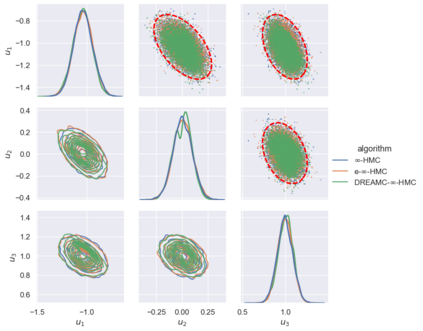
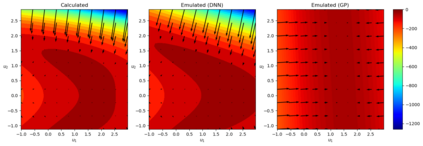
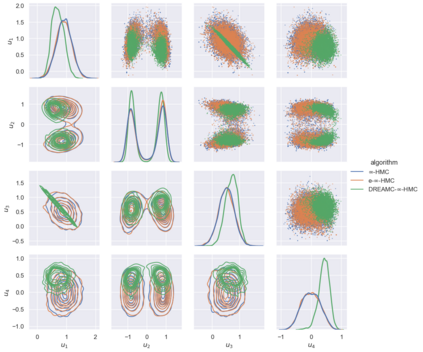
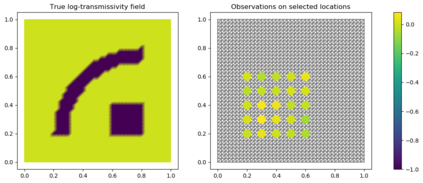
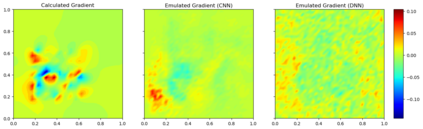
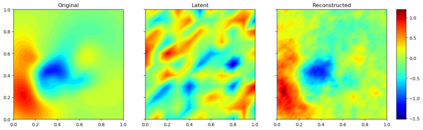
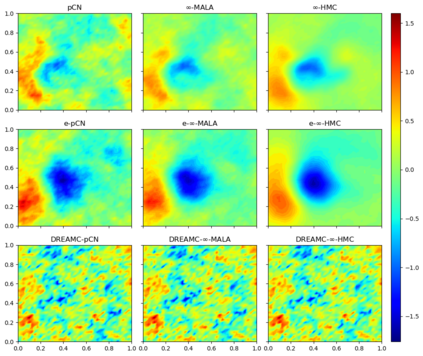
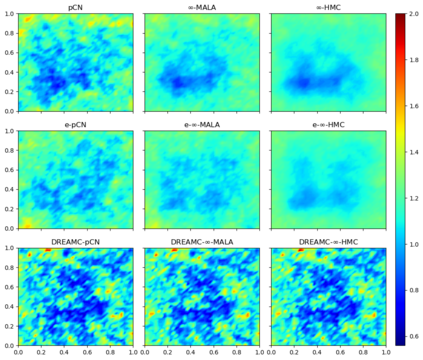
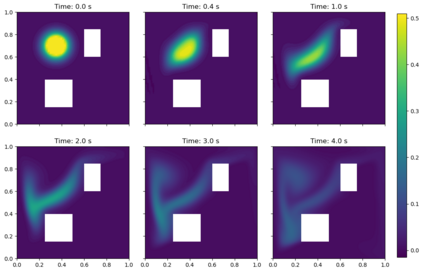
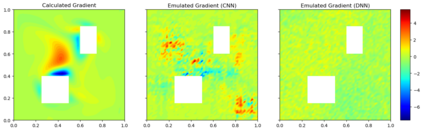
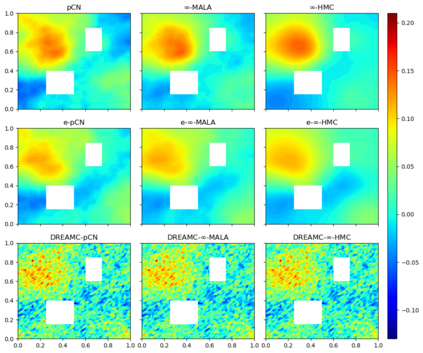
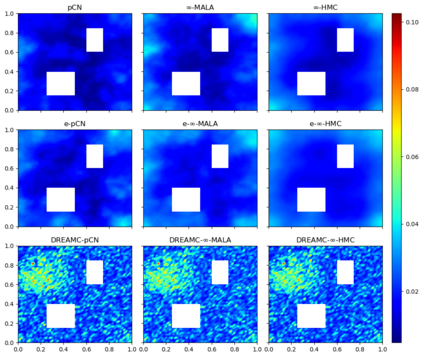
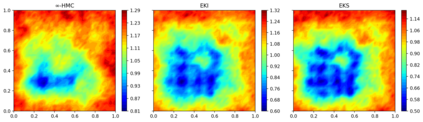
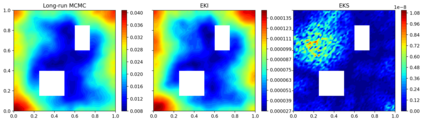
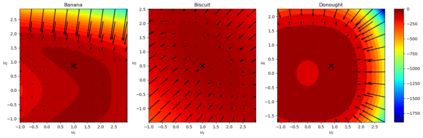
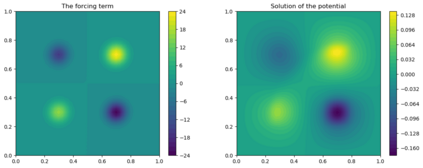
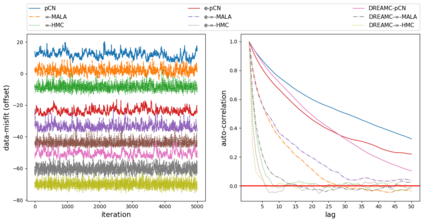
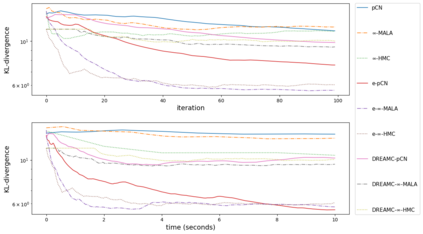
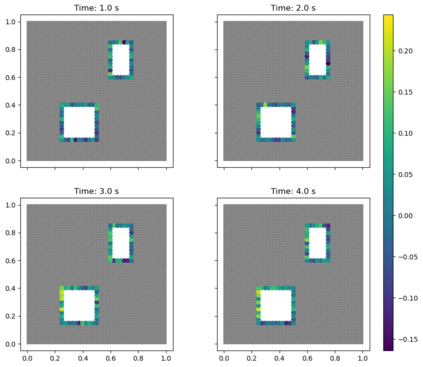
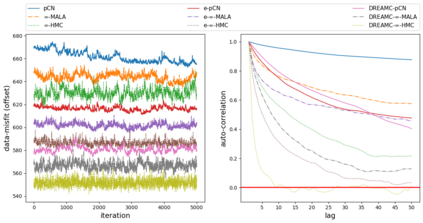
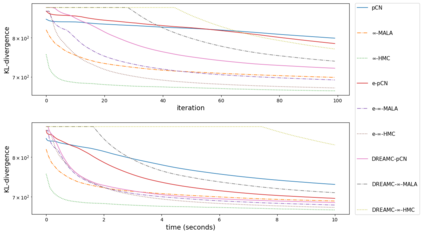
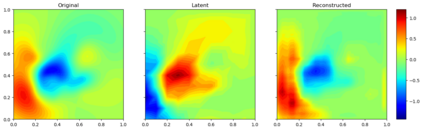
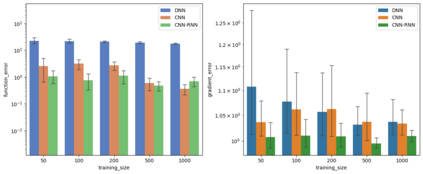
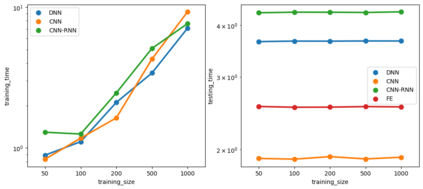
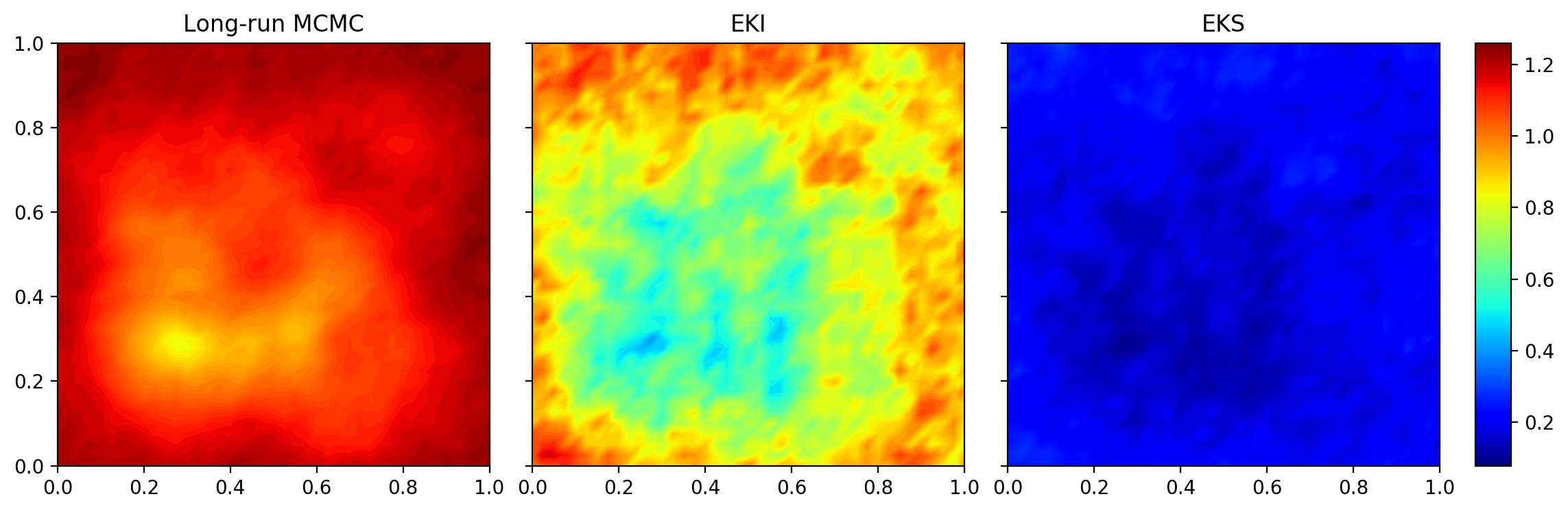
Due to the importance of uncertainty quantification (UQ), Bayesian approach to inverse problems has recently gained popularity in applied mathematics, physics, and engineering. However, traditional Bayesian inference methods based on Markov Chain Monte Carlo (MCMC) tend to be computationally intensive and inefficient for such high dimensional problems. To address this issue, several methods based on surrogate models have been proposed to speed up the inference process. More specifically, the calibration-emulation-sampling (CES) scheme has been proven to be successful in large dimensional UQ problems. In this work, we propose a novel CES approach for Bayesian inference based on deep neural network models for the emulation phase. The resulting algorithm is computationally more efficient and more robust against variations in the training set. Further, by using an autoencoder (AE) for dimension reduction, we have been able to speed up our Bayesian inference method up to three orders of magnitude. Overall, our method, henceforth called \emph{Dimension-Reduced Emulative Autoencoder Monte Carlo (DREAMC)} algorithm, is able to scale Bayesian UQ up to thousands of dimensions for inverse problems. Using two low-dimensional (linear and nonlinear) inverse problems we illustrate the validity of this approach. Next, we apply our method to two high-dimensional numerical examples (elliptic and advection-diffussion) to demonstrate its computational advantages over existing algorithms.
翻译:由于不确定性量化的重要性(UQ),巴伊西亚对反问题的方法最近在应用数学、物理和工程应用中越来越受人欢迎。然而,基于Markov链链蒙特蒙特卡洛(MCMC)的传统巴伊西亚推断方法往往在计算上密集而效率低下,以应对如此高层面的问题。为了解决这一问题,根据代用模型提出了几种方法,以加快推论过程的速度。更具体地说,校准模拟(CES)方法在大型UQ问题中被证明是成功的。在这项工作中,我们建议以深神经网络模型为基础,为模拟阶段的Bayesian推断方法提出新的CES方法。由此产生的算法在计算上效率更高且比培训设置的变异性更强。此外,通过使用自动电解码(AE)来降低尺寸,我们得以将贝伊推法的推至三个级。总体而言,我们的方法今后称为\Dimenion-Reducion Autencoder Monte-Col(DREA) 和下等方法的下两个等级,可以展示我们目前压方法的下等方法的下等方法。