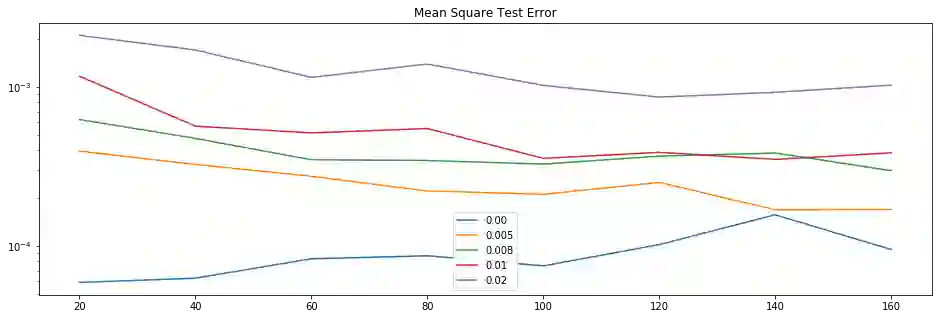
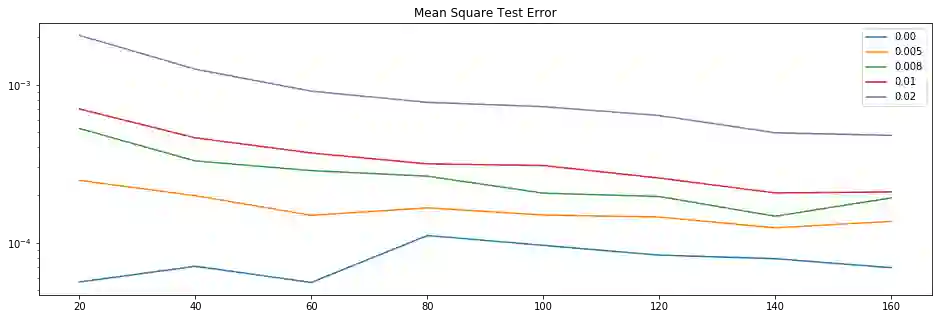
We study the problem of reconstructing solutions of inverse problems with neural networks when only noisy data is available. We assume that the problem can be modeled with an infinite-dimensional forward operator that is not continuously invertible. Then, we restrict this forward operator to finite-dimensional spaces so that the inverse is Lipschitz continuous. For the inverse operator, we demonstrate that there exists a neural network which is a robust-to-noise approximation of the operator. In addition, we show that these neural networks can be learned from appropriately perturbed training data. We demonstrate the admissibility of this approach to a wide range of inverse problems of practical interest. Numerical examples are given that support the theoretical findings.
翻译:我们研究重建神经网络反向问题解决方案的问题,只要数据繁琐,我们就会研究这个问题。我们假设,这个问题可以用一个无限的远方操作器来模拟,而远方操作器是不可不断倒置的。然后,我们把这个前方操作器限制在有限的维空间,这样反之,利普西茨是连续的。对于相反操作器,我们证明,有一个神经网络是操作器的强大至噪音近似。此外,我们还表明,这些神经网络可以从适当扰动的培训数据中学习。我们证明,这一方法可适用于一系列广泛的反面的实际问题。提供了支持理论发现的数字实例。