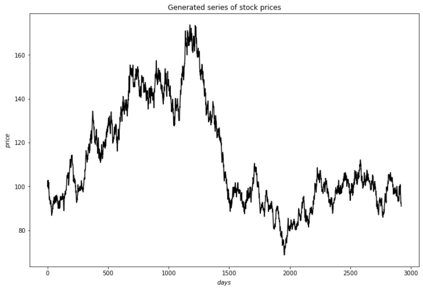
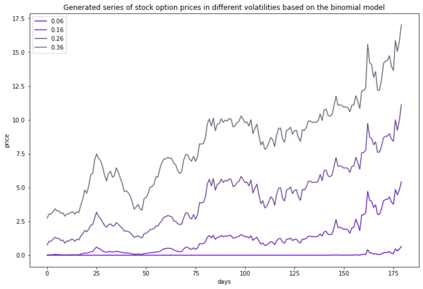
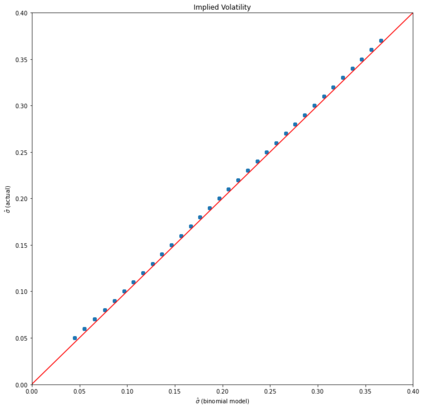
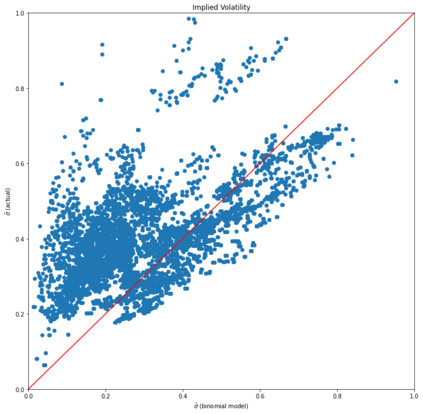
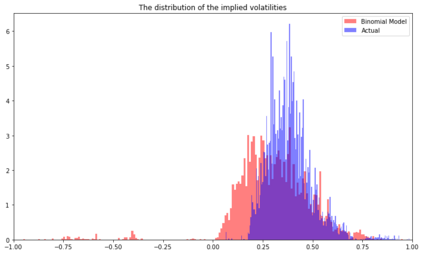
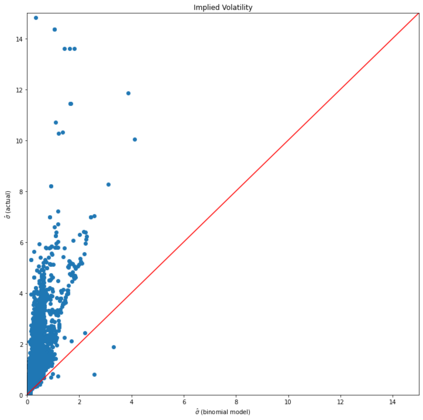
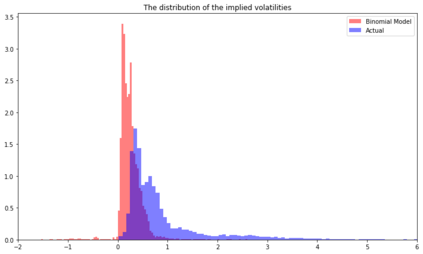
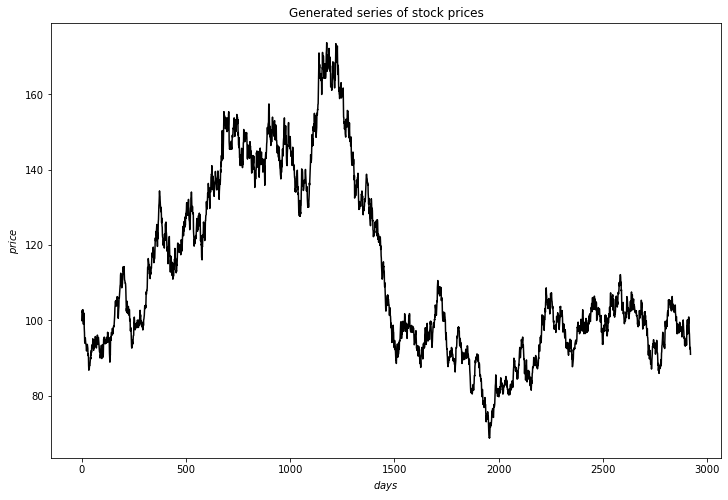
In the paper written by Klibanov et al, it proposes a novel method to calculate implied volatility of a European stock options as a solution to ill-posed inverse problem for the Black-Scholes equation. In addition, it proposes a trading strategy based on the difference between implied volatility of the option and the volatility of the underlying stock. In addition to the Black-Scholes equation, Binomial model is another method used to price European options. And, the implied volatility can be also calculated through this model. In this paper, we apply the Newton-Raphson method together with Automatic Differention to numerically approximate the implied volatility of an arbitrary stock option through this model. We provide an explanation of the mathematical model and methods, the methodology, and the results from our test using the stimulated data from the Geometric Brownian Motion Model and the Binomial Model itself, and the data from the US market data from 2018 to 2021.
翻译:在Klibanov等人撰写的论文中,它提出了一个新颖的方法,用以计算欧洲股票选择权隐含的波动性,作为解决黑色-斯科尔斯方程式中不正确反向问题的一种解决办法;此外,它还提出了一个基于选择权隐含的波动性和基础股票波动性之间的差别的贸易战略;除了黑-斯科尔斯方程式外,Binomial模型是用于给欧洲选项定价的另一种方法;也可以通过这一模型来计算隐含的波动性。在本文中,我们采用牛顿-拉夫森法和自动差异法,通过这一模型从数字上估计任意股票选择权隐含的波动性。我们解释了数学模型和方法、方法,以及我们利用从几何布朗恩模型和Binomial模型本身获得的刺激数据以及从2018年至2021年美国市场数据进行的测试的结果。