Singularity of Data Analytic Operations

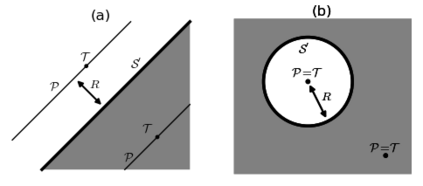
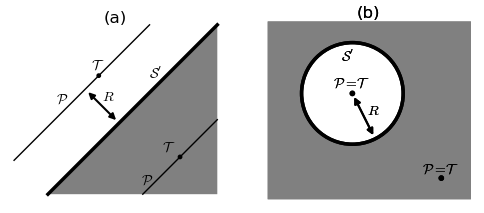
Statistical data by their very nature are indeterminate in the sense that if one repeated the process of collecting the data the new data set would be somewhat different from the original. Therefore, a statistical method, a map $\Phi$ taking a data set $x$ to a point in some space F, should be stable at $x$: Small perturbations in $x$ should result in a small change in $\Phi(x)$. Otherwise, $\Phi$ is useless at $x$ or -- and this is important -- near $x$. So one doesn't want $\Phi$ to have "singularities," data sets $x$ such that the the limit of $\Phi(y)$ as $y$ approaches $x$ doesn't exist. (Yes, the same issue arises elsewhere in applied math.) However, broad classes of statistical methods have topological obstructions of continuity: They must have singularities. We show why and give lower bounds on the Hausdorff dimension, even Hausdorff measure, of the set of singularities of such data maps. There seem to be numerous examples. We apply mainly topological methods to study the (topological) singularities of functions defined (on dense subsets of) "data spaces" and taking values in spaces with nontrivial homology. At least in this book, data spaces are usually compact manifolds. The purpose is to gain insight into the numerical conditioning of statistical description, data summarization, and inference and learning methods. We prove general results that can often be used to bound below the dimension of the singular set. We apply our topological results to develop lower bounds on Hausdorff measure of the singular set. We apply these methods to the study of plane fitting and measuring location of data on spheres. This is not a "final" version, merely another attempt.