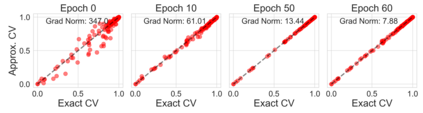
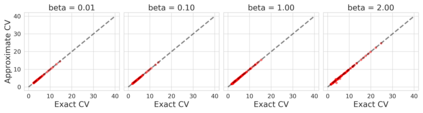
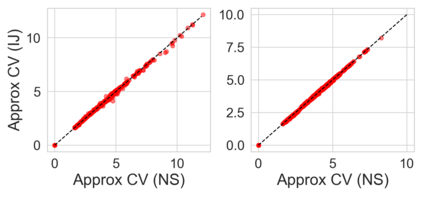
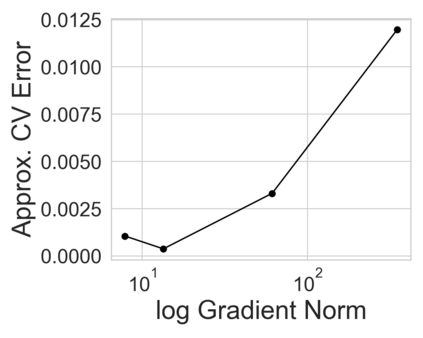
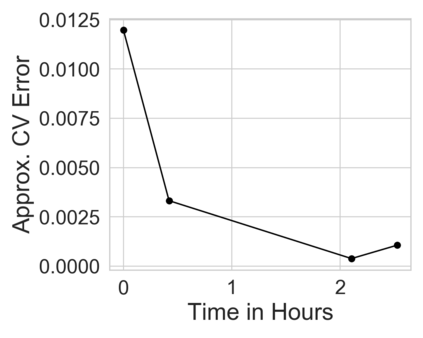
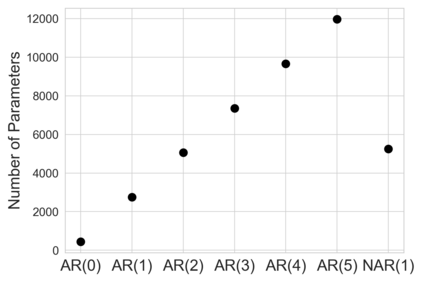
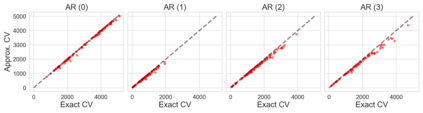
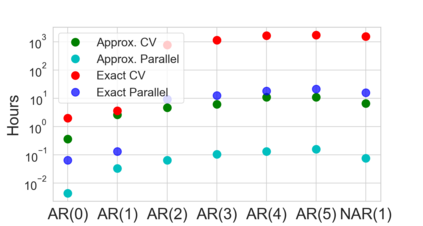
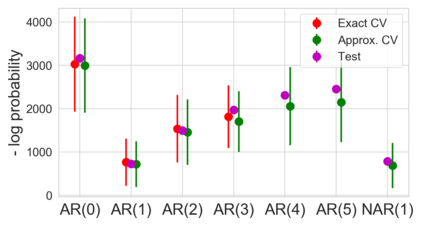
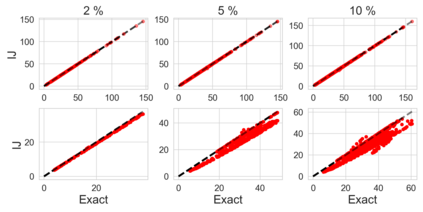
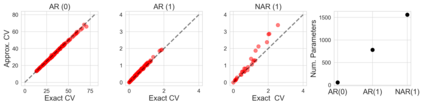
Many modern data analyses benefit from explicitly modeling dependence structure in data -- such as measurements across time or space, ordered words in a sentence, or genes in a genome. A gold standard evaluation technique is structured cross-validation (CV), which leaves out some data subset (such as data within a time interval or data in a geographic region) in each fold. But CV here can be prohibitively slow due to the need to re-run already-expensive learning algorithms many times. Previous work has shown approximate cross-validation (ACV) methods provide a fast and provably accurate alternative in the setting of empirical risk minimization. But this existing ACV work is restricted to simpler models by the assumptions that (i) data across CV folds are independent and (ii) an exact initial model fit is available. In structured data analyses, both these assumptions are often untrue. In the present work, we address (i) by extending ACV to CV schemes with dependence structure between the folds. To address (ii), we verify -- both theoretically and empirically -- that ACV quality deteriorates smoothly with noise in the initial fit. We demonstrate the accuracy and computational benefits of our proposed methods on a diverse set of real-world applications.
翻译:许多现代数据分析得益于数据中明确的依赖性结构模型化 -- -- 例如不同时间或空间的测量、句子中的定单词、或基因组中的基因。金标准评价技术是结构化的交叉验证技术,每个折叠中留有某些数据子集(例如一个时间间隔内的数据或地理区域的数据),但是,由于需要重新运行已经很昂贵的学习算法,这里的分类分析可能过于缓慢。以前的工作显示交叉验证(ACV)方法近似于交叉验证(ACV)方法,为尽量减少实证风险提供了一个快速和可辨别的准确的替代方法。但是,现有的ACV工作限于更简单的模型,其假设是:(一) 跨CV折叠的数据是独立的,和(二) 完全的初始模型是合适的。在结构化数据分析中,这两种假设往往都是不真实的。在目前的工作中,我们处理的是(一) 通过将ACV扩大为CV计划,在折叠叠中具有依赖性结构。为了解决(二),我们从理论上和实验上都核查 -- -- -- ACV质量会随着最初适合的噪音而平稳地恶化。我们提出的应用方法的精确和计算。