Approximation of discontinuous functions by Kantorovich exponential sampling series

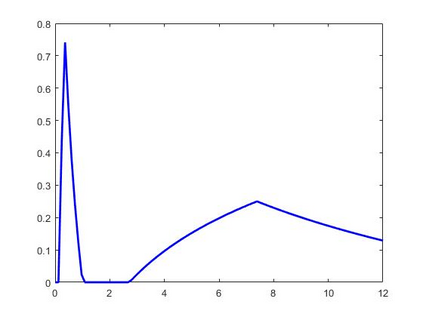
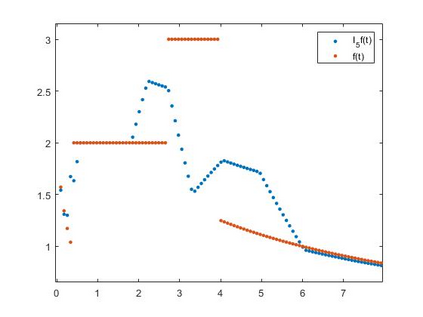
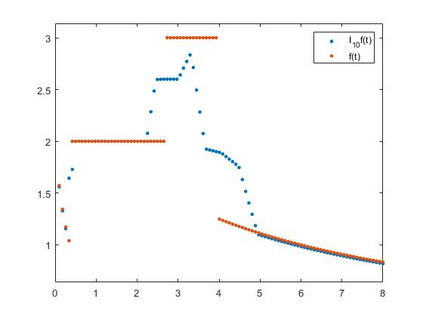
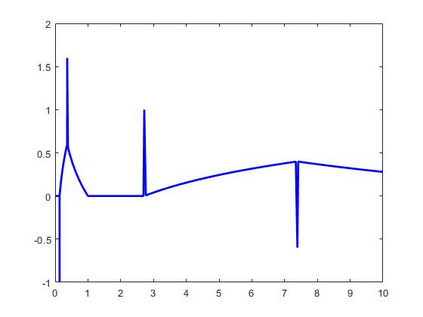
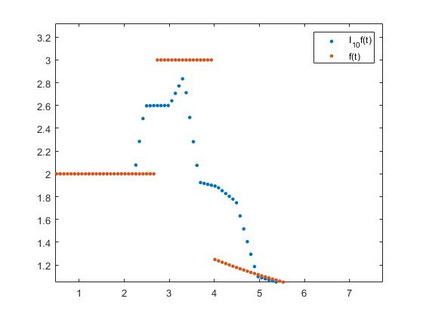
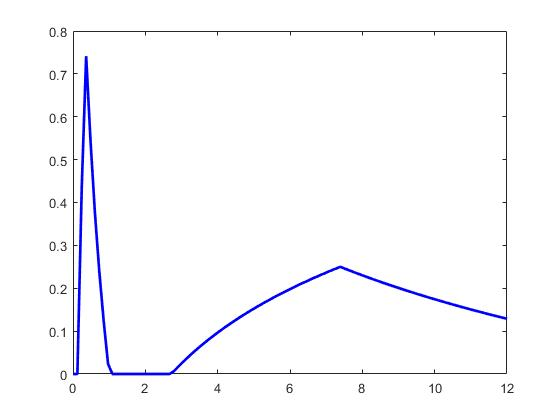
The Kantorovich exponential sampling series at jump discontinuities of the bounded measurable signal f has been analysed. A representation lemma for the series is established and using this lemma certain approximation theorems for discontinuous signals are proved. The degree of approximation in terms of logarithmic modulus of smoothness for the series is studied. Further a linear prediction of signals based on past sample values has been obtained. Some numerical simulations are performed to validate the approximation of discontinuous signals f by the sampling series.