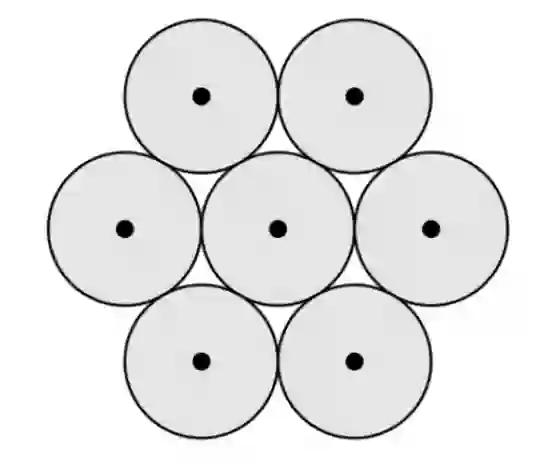
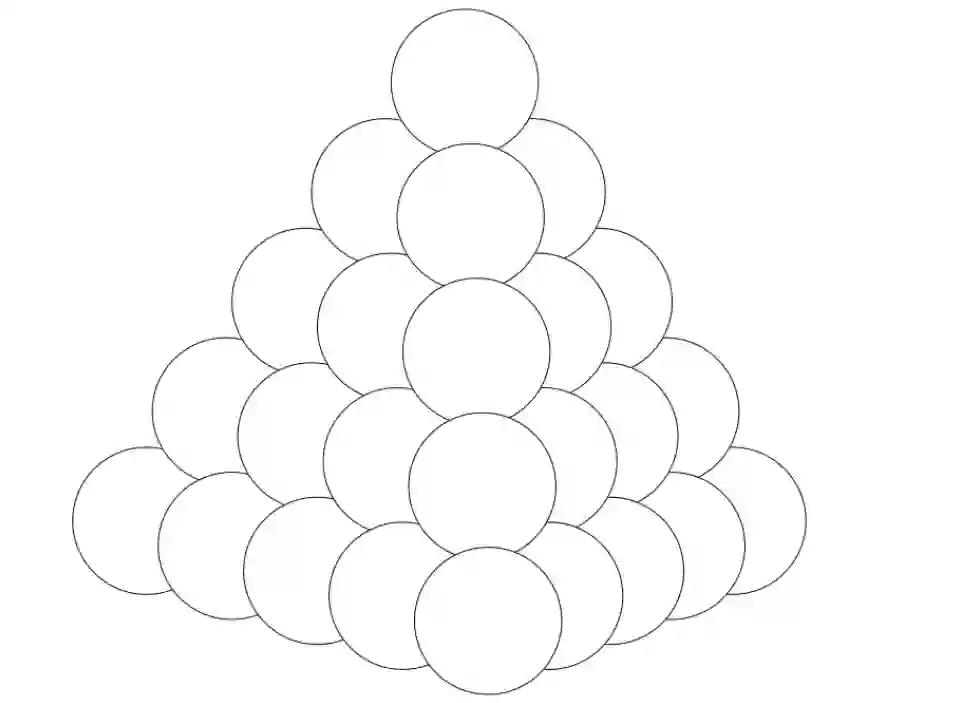
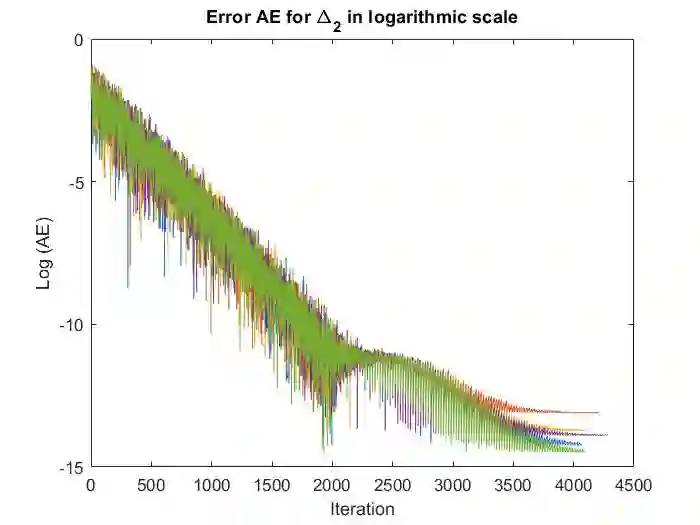
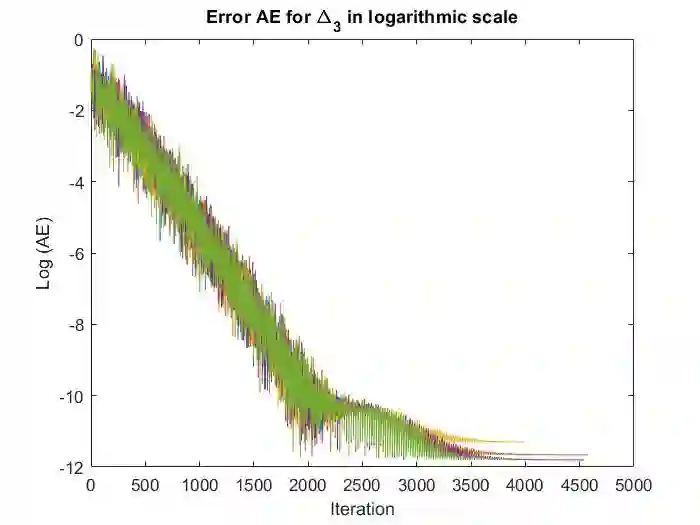
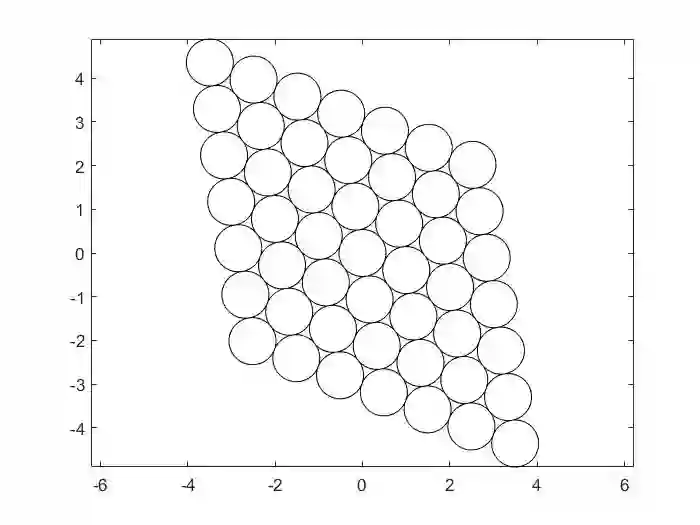
We recover the Riemannian gradient of a given function defined on interior points of a Riemannian submanifold in the Euclidean space based on a sample of function evaluations at points in the submanifold. This approach is based on the estimates of the Laplace-Beltrami operator proposed in the diffusion-maps theory. The Riemannian gradient estimates do not involve differential terms. Analytical convergence results of the Riemannian gradient expansion are proved. We apply the Riemannian gradient estimate in a gradient-based algorithm providing a derivative-free optimization method. We test and validate several applications, including tomographic reconstruction from an unknown random angle distribution, and the sphere packing problem in dimensions 2 and 3.
翻译:我们根据对欧洲极地空间里格曼尼亚梯度的内部点的抽样功能评价,回收了在欧几里德空间里格曼尼亚梯度内点界定的某一功能的里格曼尼梯度,这一方法基于扩散分布图理论中提议的Laplace-Beltrami操作员的估计数。里格曼尼尼亚梯度估计数不涉及不同条件。里格曼尼梯度扩大的分析趋同结果得到证明。我们用基于梯度的算法使用里欧曼尼梯度估计值,提供一种无衍生物优化方法。我们测试和验证了若干应用,包括从未知的随机角度分布进行地形重建,以及第2和第3维的球体包装问题。我们测试和验证了若干应用,包括从未知的随机角度分布进行地形重建。