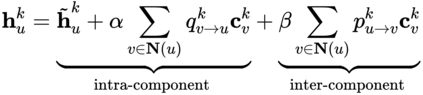
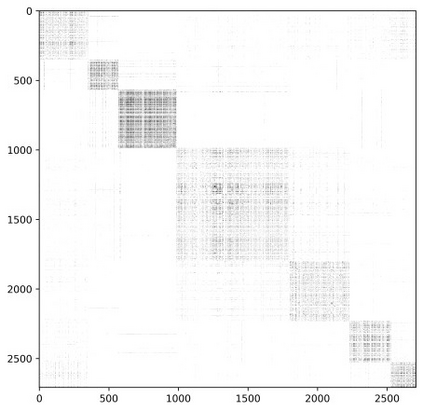
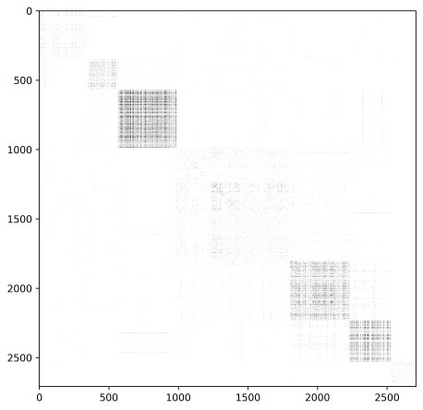
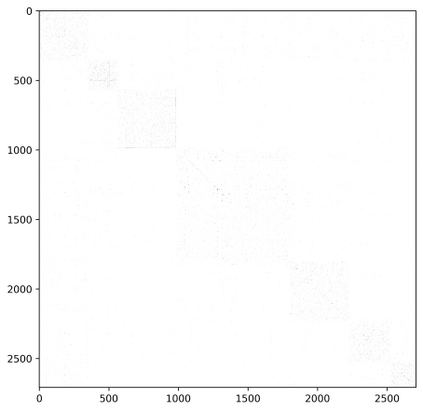
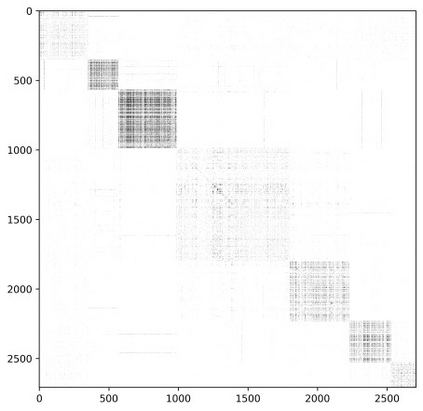
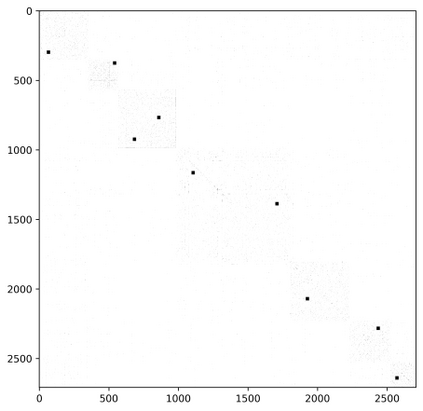
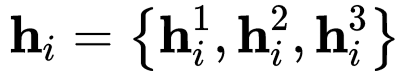A real-world graph has a complex topological structure, which is often formed by the interaction of different latent factors. Disentanglement of these latent factors can effectively improve the robustness and expressiveness of node representation of graph. However, most existing methods lack consideration of the intrinsic differences in relations between nodes caused by factor entanglement. In this paper, we propose an Adversarial Disentangled Graph Convolutional Network (ADGCN) for disentangled graph representation learning. Specifically, a component-specific aggregation approach is proposed to achieve micro-disentanglement by inferring latent components that caused the links between nodes. On the basis of micro-disentanglement, we further propose a macro-disentanglement adversarial regularizer to improve the separability among component distributions, thus restricting the interdependence among components. Additionally, to reveal the topological graph structure, a diversity-preserving node sampling approach is proposed, by which the graph structure can be progressively refined in a way of local structure awareness. The experimental results on various real-world graph data verify that our ADGCN obtains more favorable performance over currently available alternatives.
翻译:真实世界图是一个复杂的表层结构,通常由不同潜在因素的相互作用组成。这些潜在因素的分解能够有效地改善图中节点代表的坚固性和表现性。然而,大多数现有方法没有考虑到因因素缠绕而导致的节点之间关系的内在差异。在本文件中,我们建议建立一个反向分解的图表相交网络(ADGCN),用于分解图形代表学习。具体地说,建议采用一个针对具体组成部分的汇总方法,通过推断导致节点之间联系的潜在组成部分来实现微观分解。在微分分分法的基础上,我们进一步提出一个宏观分解的对立调节器,以改善各部分分布之间的分离性,从而限制各组成部分之间的相互依存性。此外,为了揭示表层图结构,我们提出了一种多样性保留节点的抽样方法,通过这种方法可以逐渐改进图表结构,以了解当地结构。各种真实世界图表数据的实验结果证实,我们的ADGCN获得了比现有替代方法更有利的性。