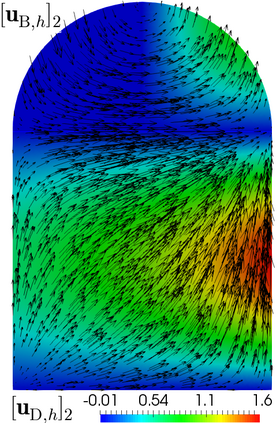
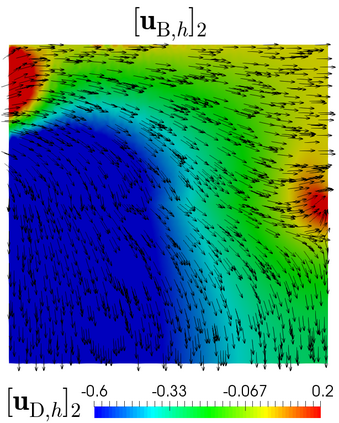
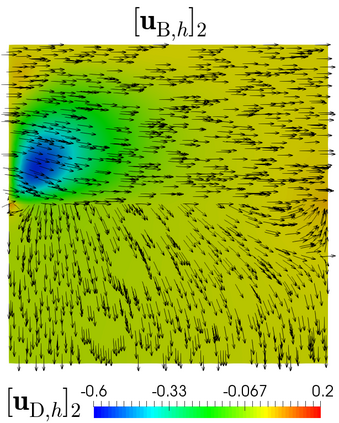
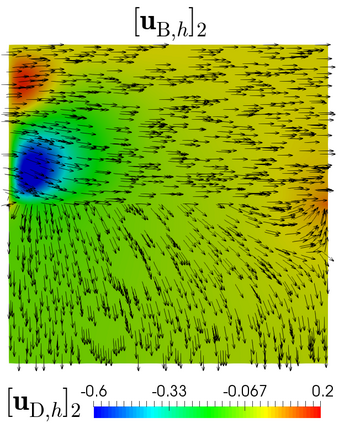
This paper develops the a priori analysis of a mixed finite element method for the filtration of an incompressible fluid through a non-deformable saturated porous medium with heterogeneous permeability. Flows are governed by the Brinkman--Forchheimer and Darcy equations in the more and less permeable regions, respectively, and the corresponding transmission conditions are given by mass conservation and continuity of momentum. We consider the standard mixed formulation in the Brinkman--Forchheimer domain and the dual-mixed one in the Darcy region, and we impose the continuity of the normal velocities by introducing suitable Lagrange multiplier. The finite element discretization involves Bernardi--Raugel and Raviart--Thomas elements for the velocities, piecewise constants for the pressures, and continuous piecewise linear elements for the Lagrange multiplier. Stability, convergence, and a priori error estimates for the associated Galerkin scheme are obtained. Numerical tests illustrate the theoretical results.
翻译:本文先验地分析了通过不畸形的饱和多孔多孔介质过滤不压缩液体的混合限值元素方法,该介质可渗透性介质各异。流动分别由渗透性较弱的地区的布林克曼-福赫海默和达西方程式管理,相应的传输条件则由大规模保护和势头的连续性提供。我们考虑了布林克曼-福赫海默域的标准混合配方和达西区域内的双混合配方,我们通过引入合适的拉格朗倍增效法,将正常速度的连续性强加于我们。最小的分解元素包括速度元素的伯纳迪-劳格尔和拉维亚特-图马斯元元素,压力的整数常数,以及拉格兰奇乘数的连续片分线元素。我们获得了相关加勒金办法的稳定、趋同和前置误差估计。数值测试说明了理论结果。
相关内容
Source: Apple - iOS 8