Blind Two-Dimensional Super-Resolution and Its Performance Guarantee (Extended Version)

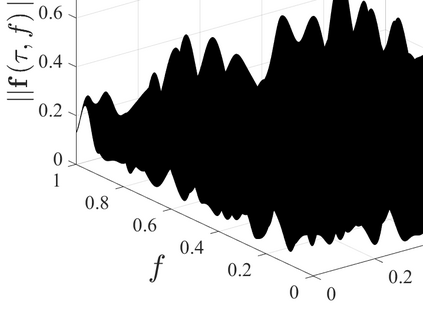
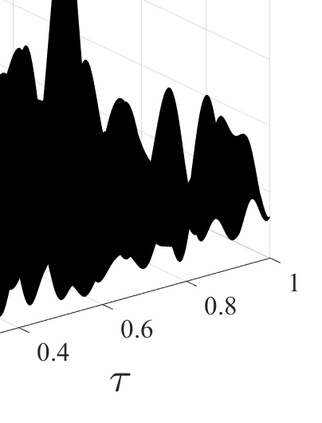
We study the problem of identifying the parameters of a linear system from its response to multiple unknown waveforms. We assume that the system response is a scaled superposition of time-delayed and frequency-shifted versions of the unknown waveforms. Such kind of problem is severely ill-posed and does not yield a unique solution without introducing further constraints. To fully characterize the system, we assume that the unknown waveforms lie in a common known low-dimensional subspace that satisfies certain properties. Then, we develop a blind two-dimensional (2D) super-resolution framework that applies to a large number of applications. In this framework, we show that under a minimum separation between the time-frequency shifts, all the unknowns that characterize the system can be recovered precisely and with high probability provided that a lower bound on the number of the observed samples is satisfied. The proposed framework is based on a 2D atomic norm minimization problem, which is shown to be reformulated and solved via semidefinite programming. Simulation results that confirm the theoretical findings of the paper are provided.