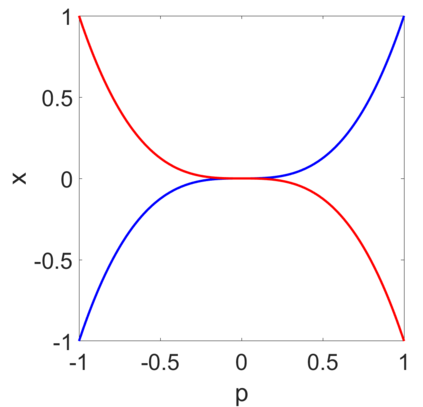
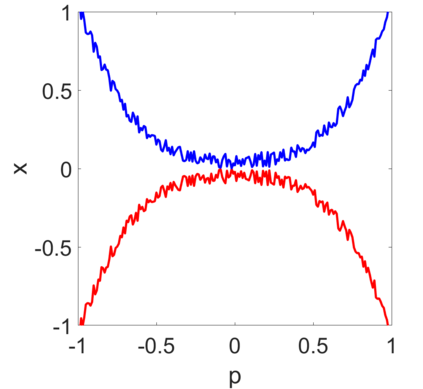
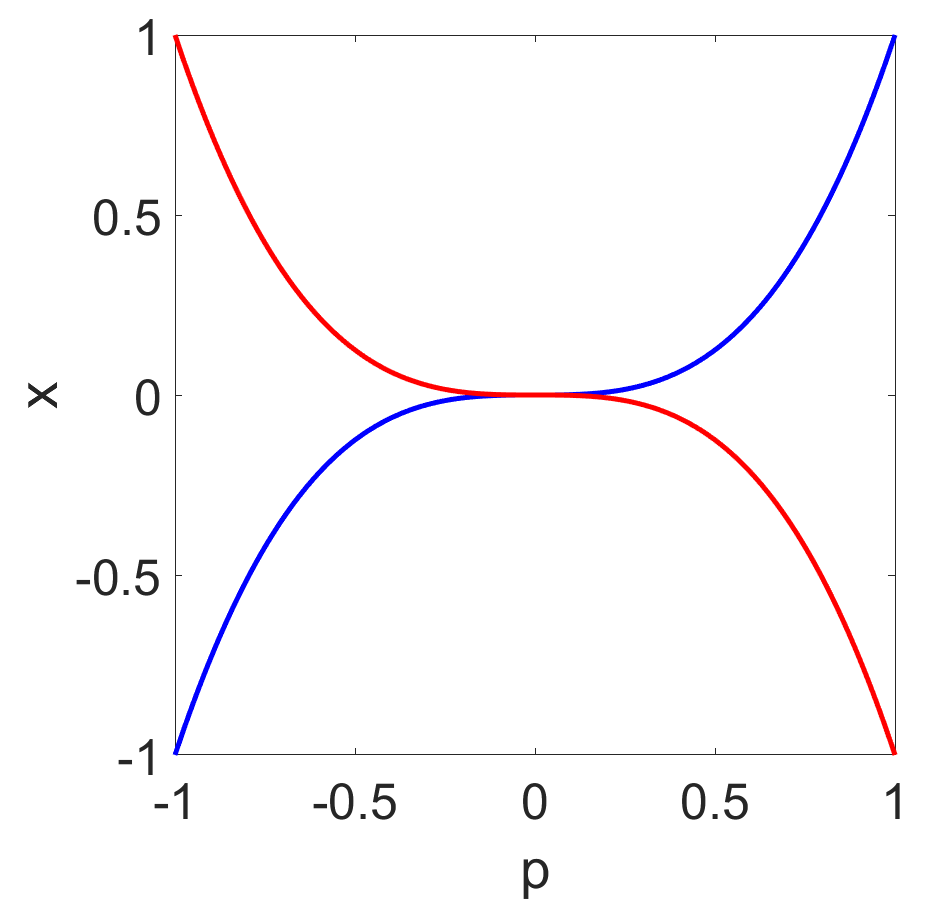
The homotopy continuation method has been widely used in solving parametric systems of nonlinear equations. But it can be very expensive and inefficient due to singularities during the tracking even though both start and end points are non-singular. The current tracking algorithms focus on the adaptivity of the stepsize by estimating the distance to the singularities but cannot avoid these singularities during the tracking. We present a stochastic homotopy tracking algorithm that perturbs the original parametric system randomly each step to avoid the singularities. We then prove that the stochastic solution path introduced by this new method is still closed to the original solution path theoretically. Moreover, several homotopy examples have been tested to show the efficiency of the stochastic homotopy tracking method.
翻译:在解决非线性方程式的参数系统时,广泛使用了同质继续使用的方法。但由于跟踪过程中的奇点(即使起始点和终点都是非同质的),这种方法可能非常昂贵,效率也很低。目前的跟踪算法通过估计与奇点的距离,侧重于步骤化的适应性,但是在跟踪过程中无法避免这些奇点。我们提出了一个随机破坏原始的参数系统的同质性跟踪算法,以避免奇点。然后我们证明,这一新方法引入的随机解决方案路径在理论上仍然关闭在原始解决方案路径上。此外,一些同质性实例已经测试,以显示同质性同质跟踪方法的效率。