Tracking Changing Probabilities via Dynamic Learners

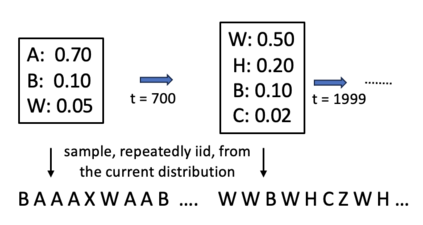
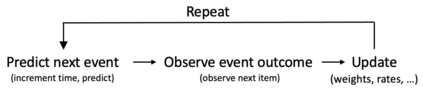
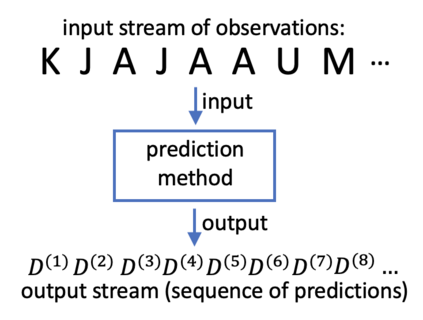
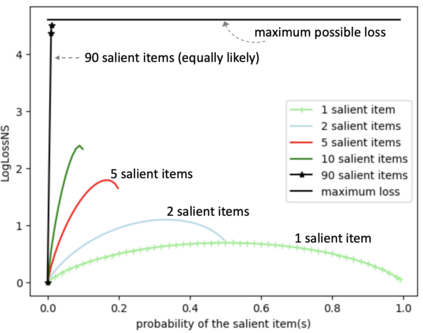
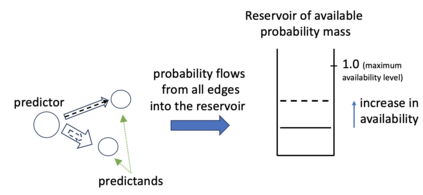
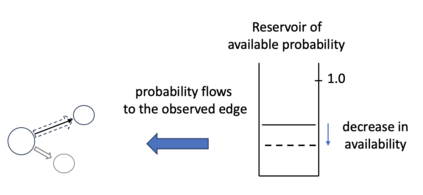
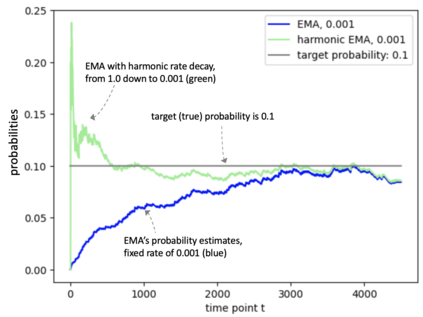
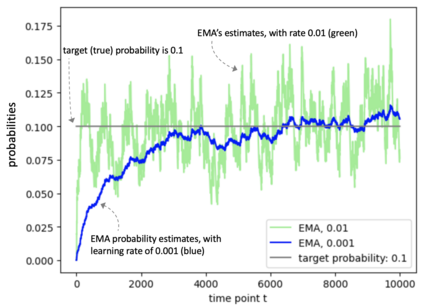
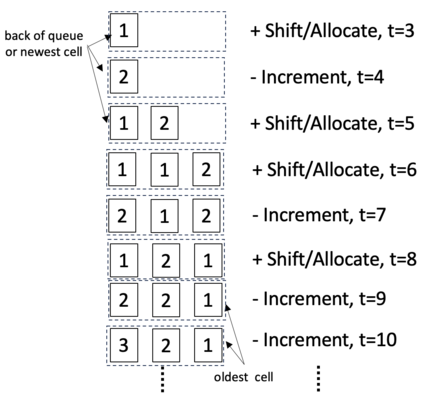
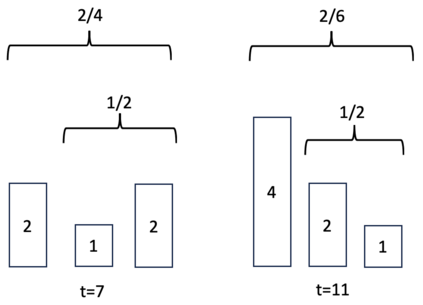
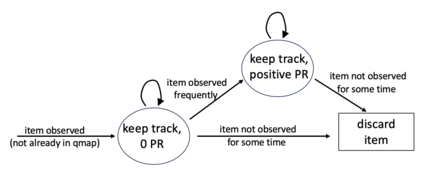
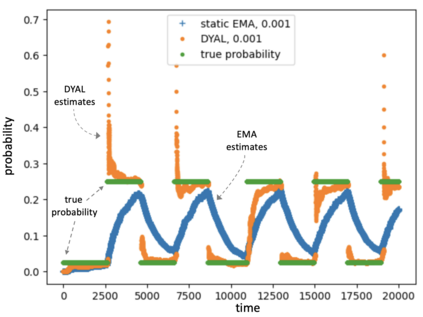
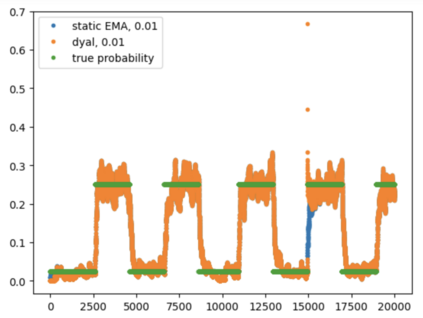
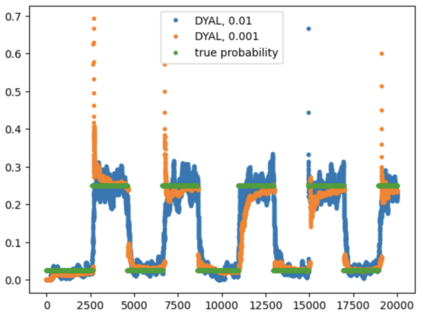
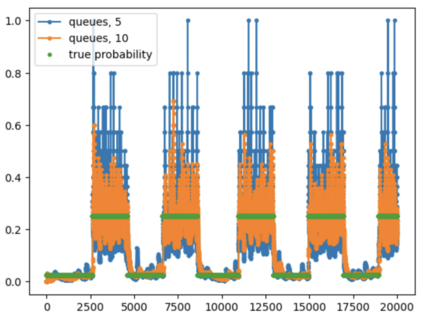
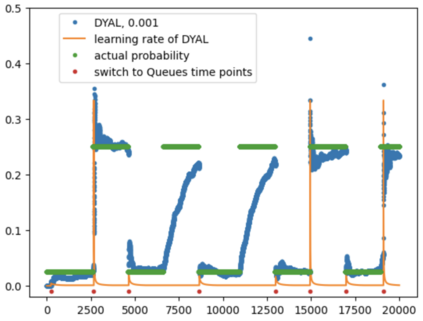
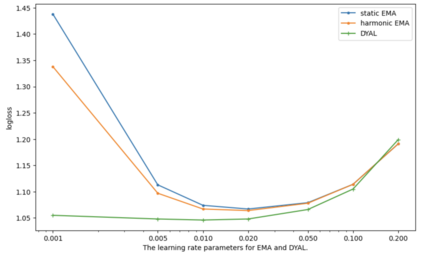
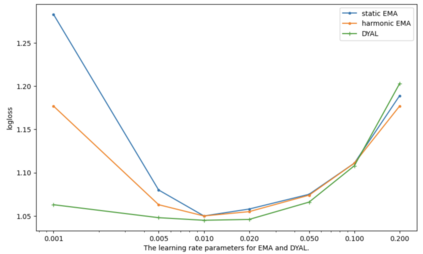
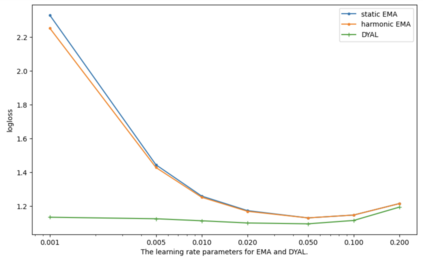
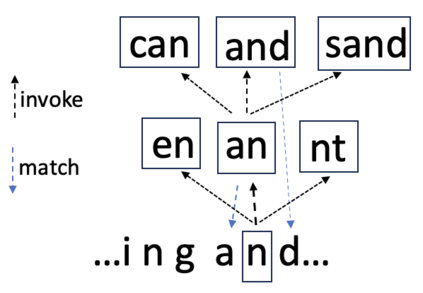
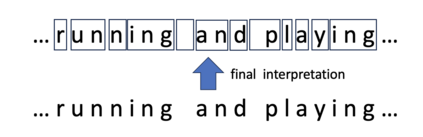
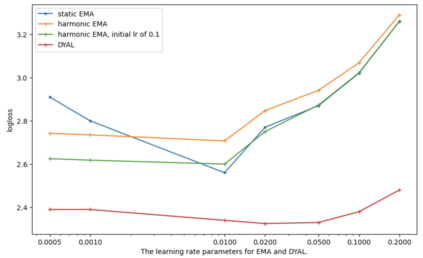
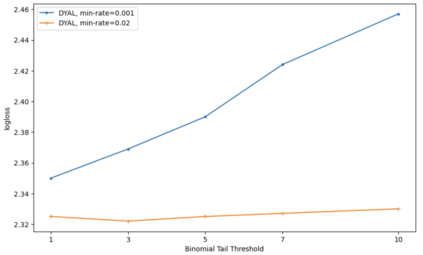
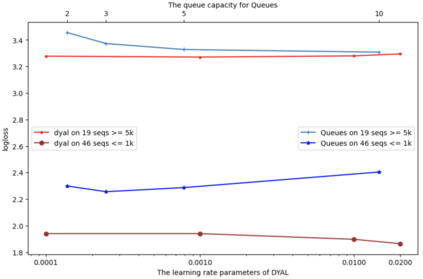
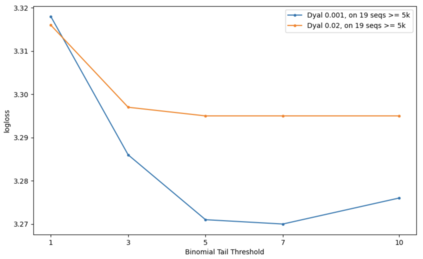
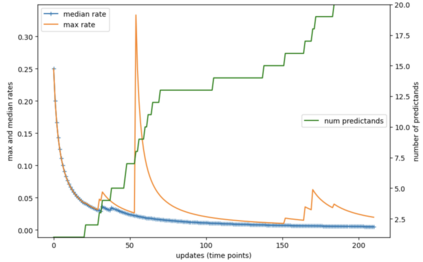
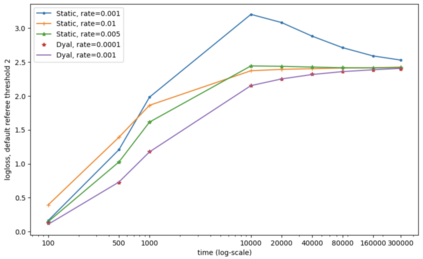
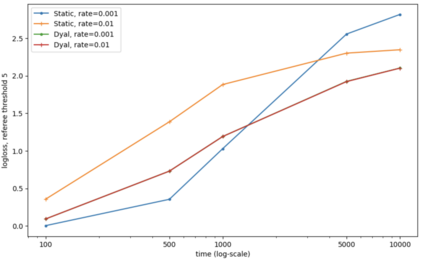
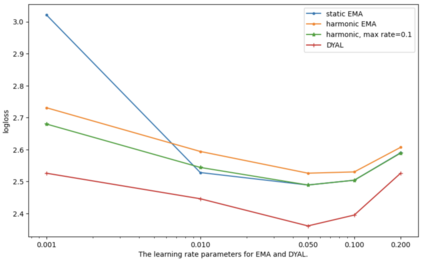
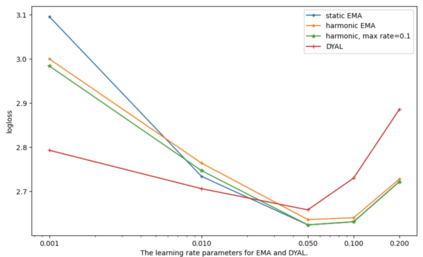
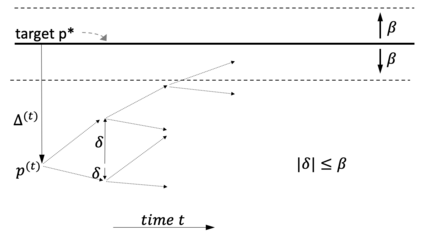
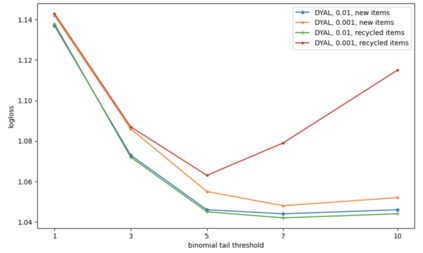
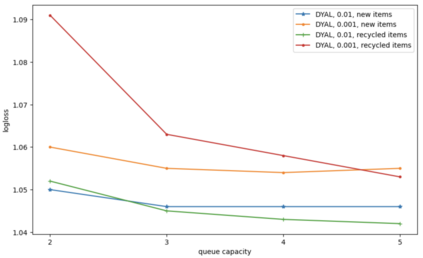
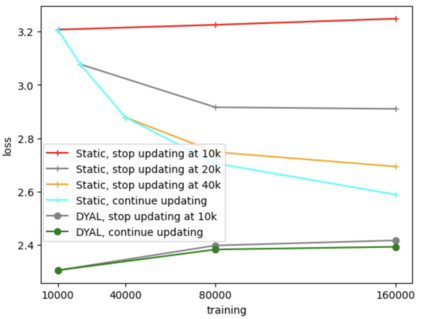
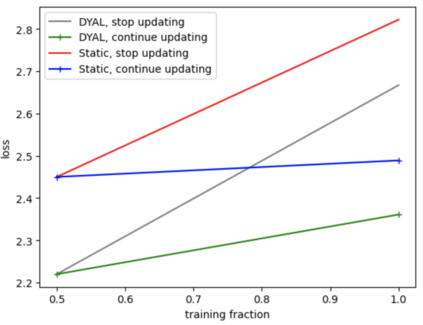
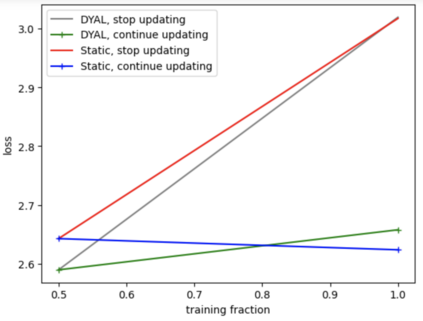
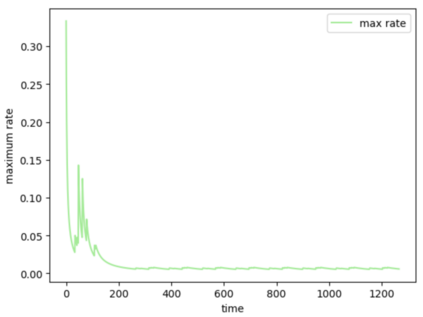
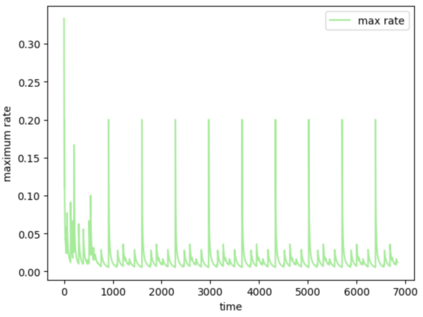
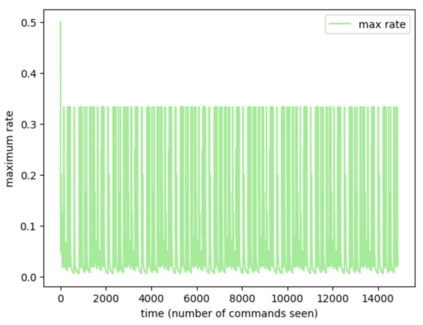
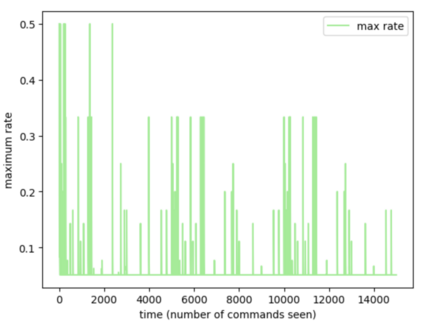
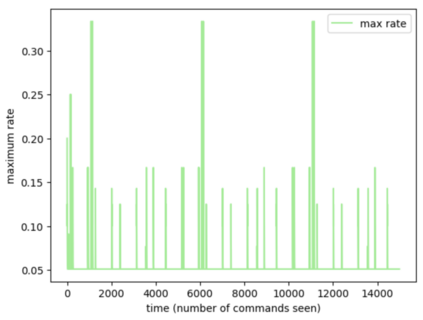
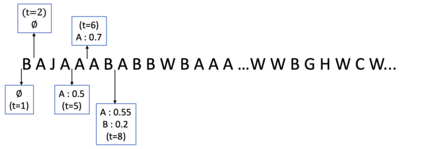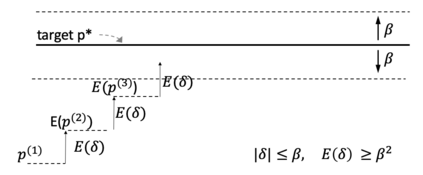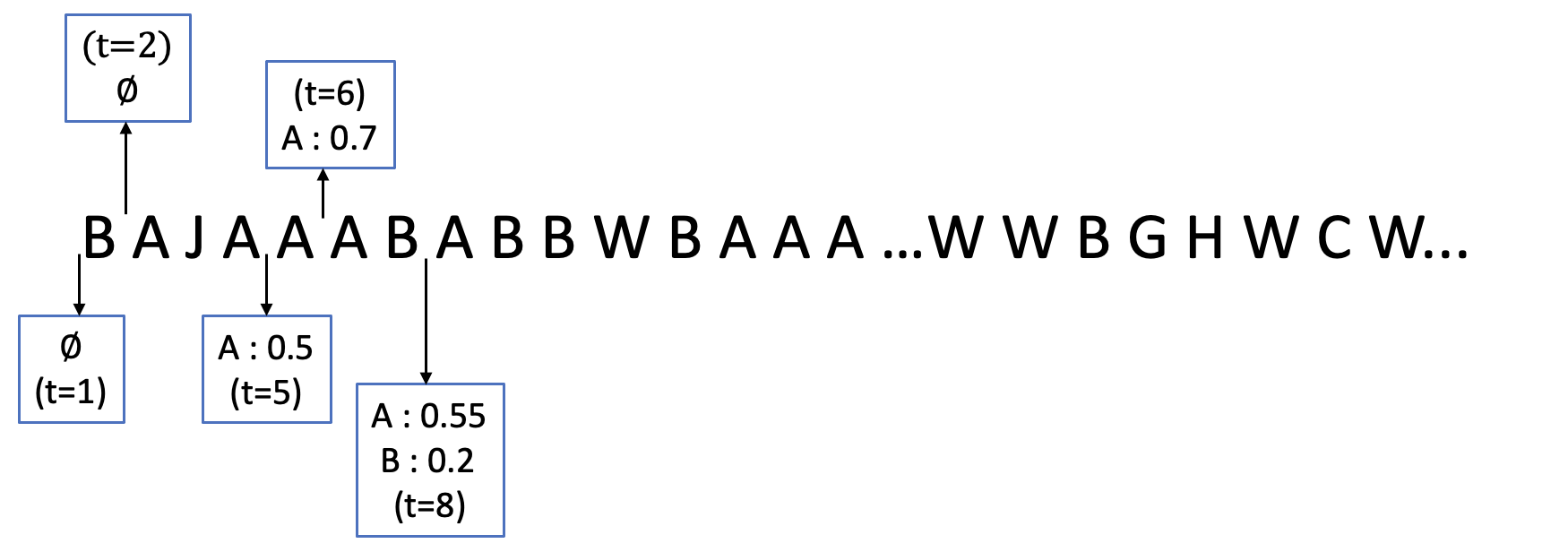Consider a predictor, a learner, whose input is a stream of discrete items. The predictor's task, at every time point, is probabilistic multiclass prediction, i.e., to predict which item may occur next by outputting zero or more candidate items, each with a probability, after which the actual item is revealed and the predictor learns from this observation. To output probabilities, the predictor keeps track of the proportions of the items it has seen. The predictor has constant (limited) space and we seek efficient prediction and update techniques: The stream is unbounded, the set of items is unknown to the predictor and their totality can also grow unbounded. Moreover, there is non-stationarity: the underlying frequencies of items may change, substantially, from time to time. For instance, new items may start appearing and a few currently frequent items may cease to occur again. The predictor, being space-bounded, need only provide probabilities for those items with (currently) sufficiently high frequency, i.e., the salient items. This problem is motivated in the setting of prediction games, a self-supervised learning regime where concepts serve as both the predictors and the predictands, and the set of concepts grows over time, resulting in non-stationarities as new concepts are generated and used. We develop moving average techniques designed to respond to such non-stationarities in a timely manner, and explore their properties. One is a simple technique based on queuing of count snapshots, and another is a combination of queuing together with an extended version of sparse EMA. The latter combination supports predictand-specific dynamic learning rates. We find that this flexibility allows for a more accurate and timely convergence.