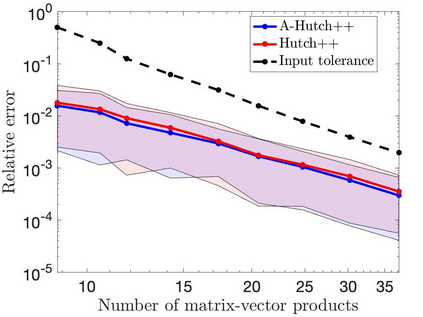
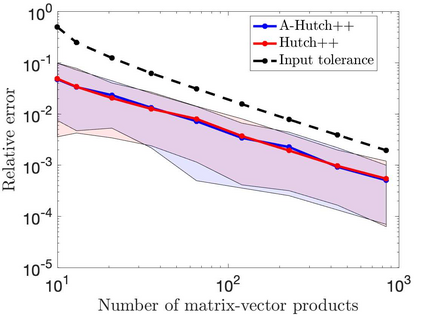
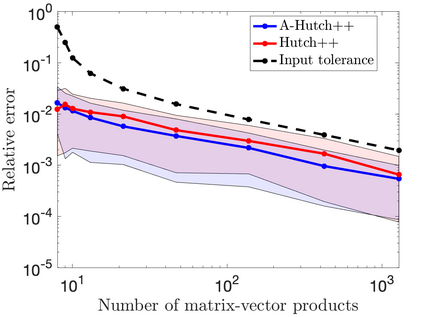
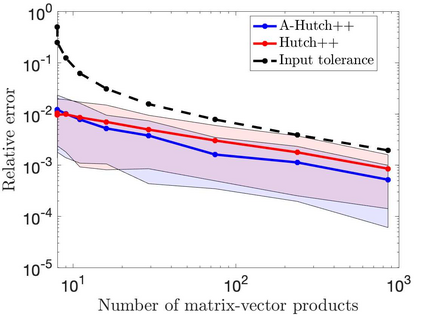
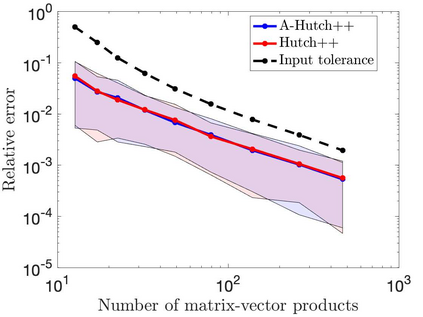
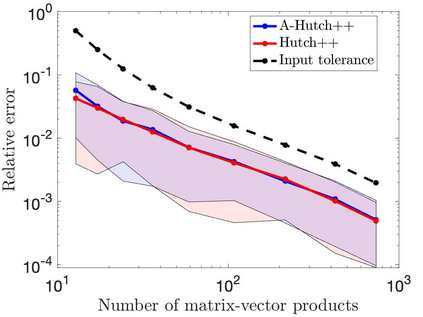
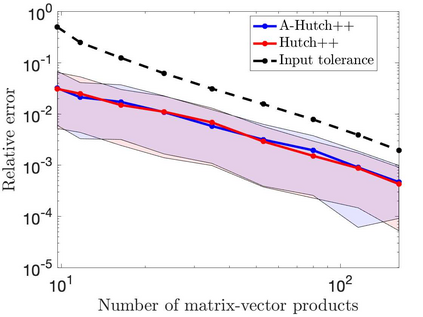
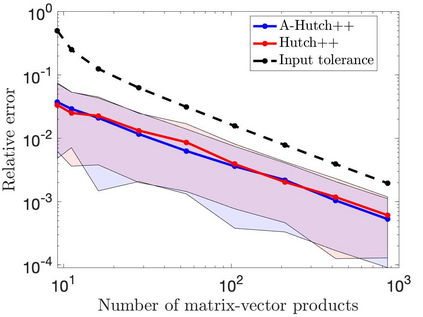
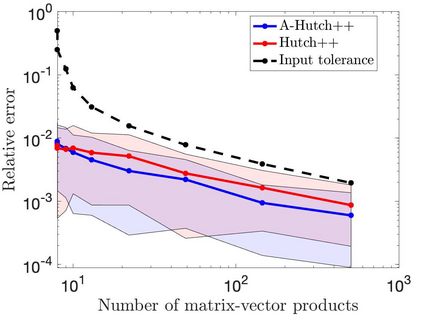
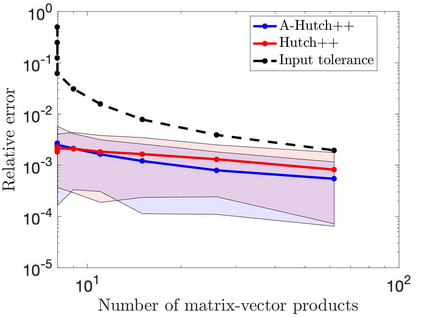
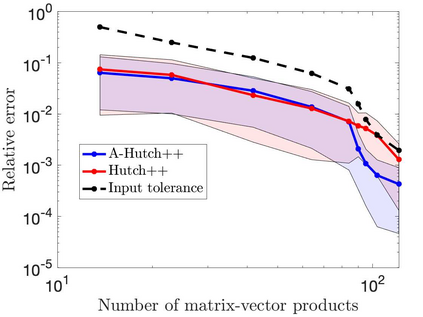
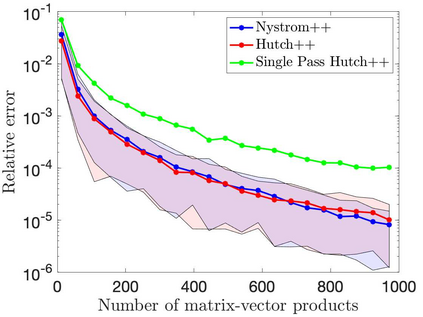
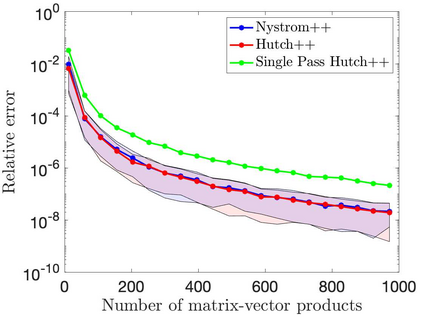
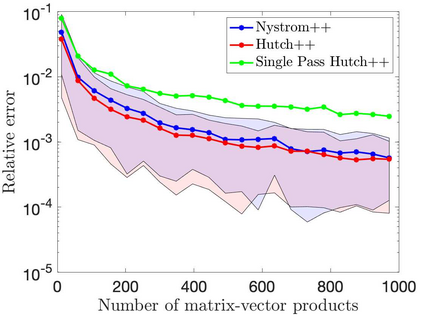
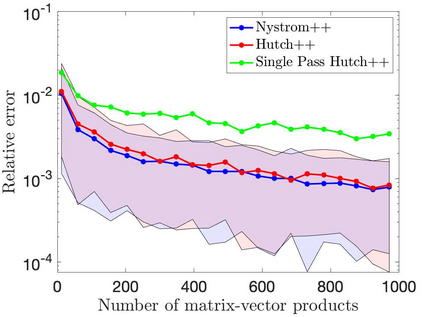
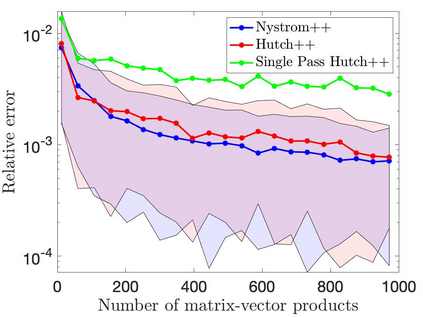
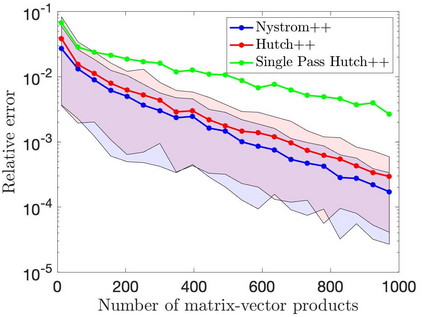
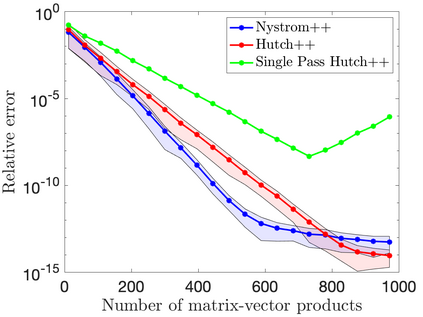
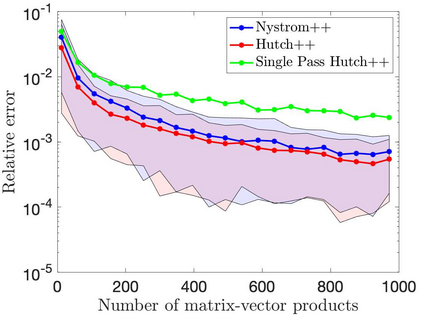
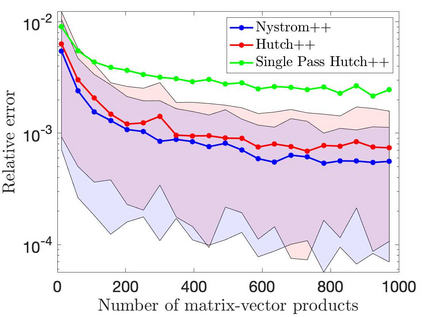
This paper is concerned with two improved variants of the Hutch++ algorithm for estimating the trace of a square matrix, implicitly given through matrix-vector products. Hutch++ combines randomized low-rank approximation in a first phase with stochastic trace estimation in a second phase. In turn, Hutch++ only requires $O\left(\varepsilon^{-1}\right)$ matrix-vector products to approximate the trace within a relative error $\varepsilon$ with high probability. This compares favorably with the $O\left(\varepsilon^{-2}\right)$ matrix-vector products needed when using stochastic trace estimation alone. In Hutch++, the number of matrix-vector products is fixed a priori and distributed in a prescribed fashion among the two phases. In this work, we derive an adaptive variant of Hutch++, which outputs an estimate of the trace that is within some prescribed error tolerance with a controllable failure probability, while splitting the matrix-vector products in a near-optimal way among the two phases. For the special case of symmetric positive semi-definite matrix, we present another variant of Hutch++, called Nystr\"om++, which utilizes the so called Nystr\"om approximation and requires only one pass over the matrix, as compared to two passes with Hutch++. We extend the analysis of Hutch++ to Nystr\"om++. Numerical experiments demonstrate the effectiveness of our two new algorithms.
翻译:本文关注 Hutch++ 算法的两个改进变体, 以估算平方矩阵的痕量。 Hutch++ 将第一阶段随机的低端近似值与第二阶段的随机性跟踪估计结合起来。 反过来, Hutch+ 只要求 $Oleft (\\ varepsilón\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\Right) 矩阵- Vlight 值产品, 以高概率来估计相对差错差数。 这与 $Or\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\