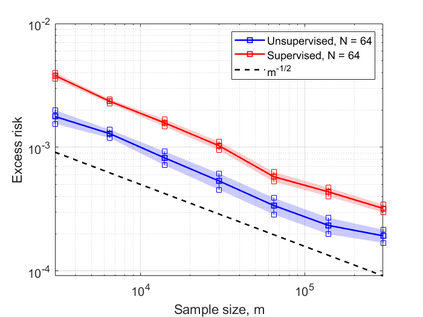
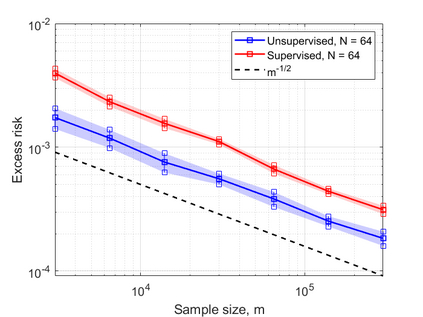
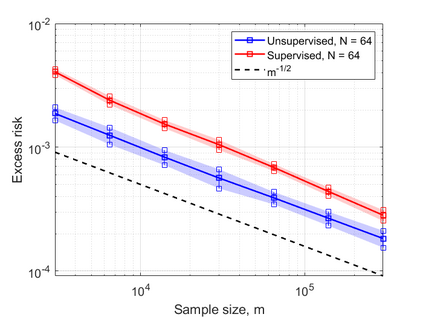
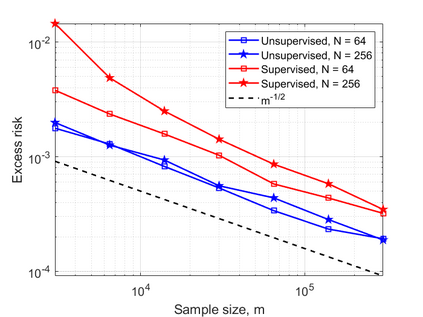
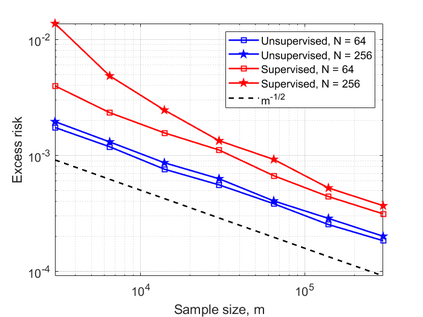
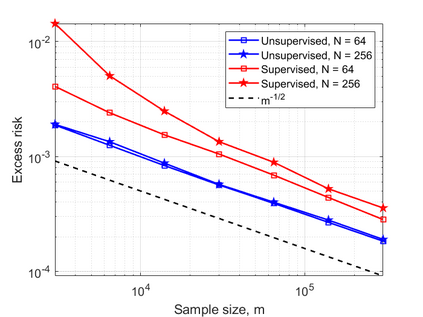
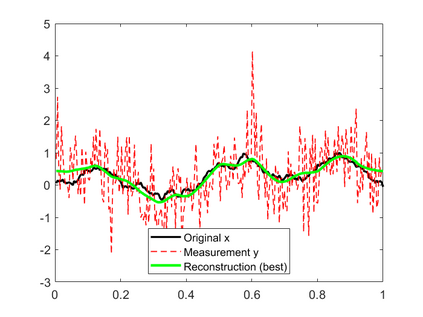
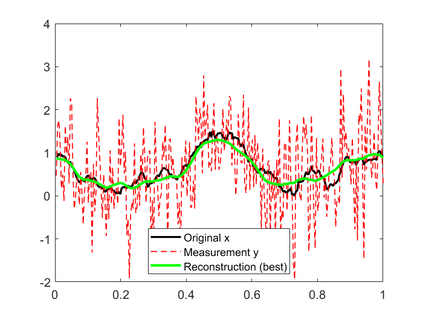
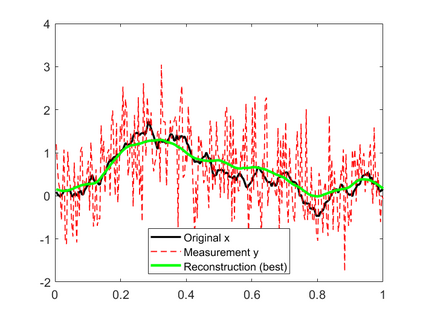
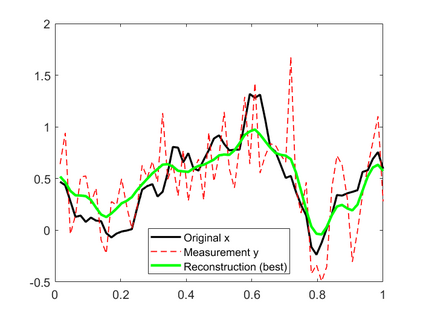
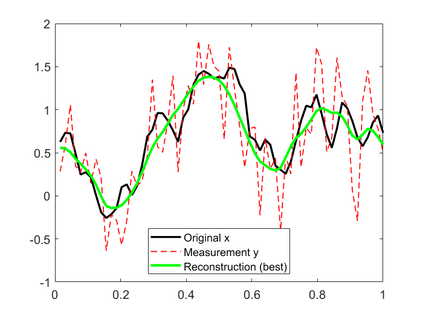
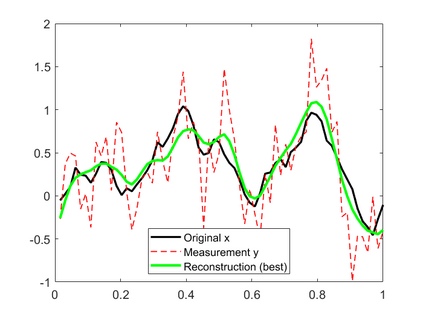
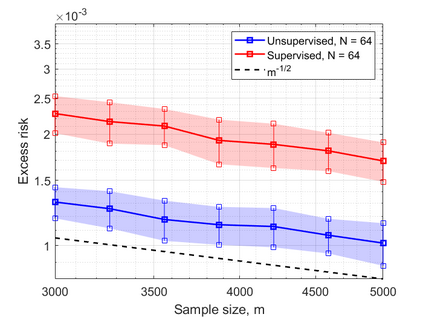
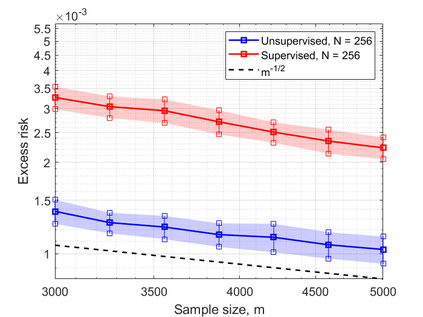
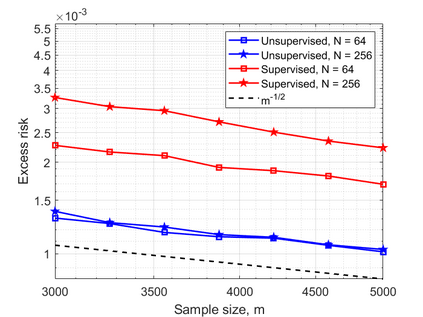
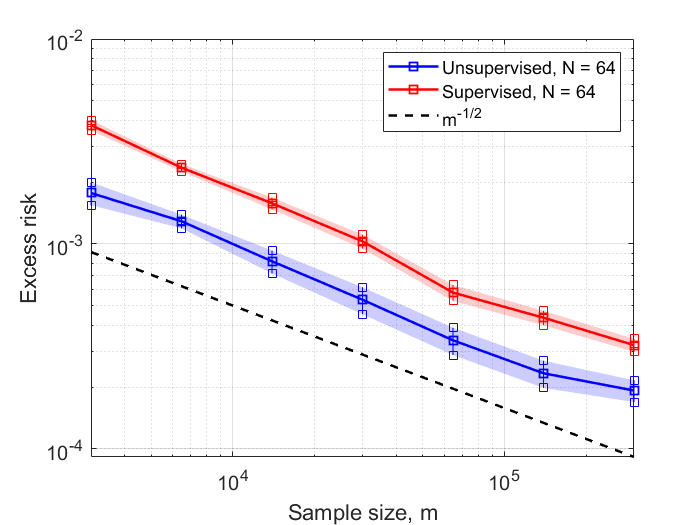
In this work, we consider the linear inverse problem $y=Ax+\epsilon$, where $A\colon X\to Y$ is a known linear operator between the separable Hilbert spaces $X$ and $Y$, $x$ is a random variable in $X$ and $\epsilon$ is a zero-mean random process in $Y$. This setting covers several inverse problems in imaging including denoising, deblurring, and X-ray tomography. Within the classical framework of regularization, we focus on the case where the regularization functional is not given a priori but learned from data. Our first result is a characterization of the optimal generalized Tikhonov regularizer, with respect to the mean squared error. We find that it is completely independent of the forward operator $A$ and depends only on the mean and covariance of $x$. Then, we consider the problem of learning the regularizer from a finite training set in two different frameworks: one supervised, based on samples of both $x$ and $y$, and one unsupervised, based only on samples of $x$. In both cases, we prove generalization bounds, under some weak assumptions on the distribution of $x$ and $\epsilon$, including the case of sub-Gaussian variables. Our bounds hold in infinite-dimensional spaces, thereby showing that finer and finer discretizations do not make this learning problem harder. The results are validated through numerical simulations.
翻译:在这项工作中,我们考虑到线性反问题$y=Ax ⁇ epsilon$, 美元A\cron X_to Y$是已知的分解的Hilbert空间之间的线性操作员,美元X1美元和美元Y1美元,美元x是一个随机的变数,美元美元和美元=efsilon$是一个零平均随机过程。这个设置涉及成像方面的几个反问题,包括解译、分解和X光照相。在典型的正规化框架内,我们侧重于正规化功能不是先验的,而是从数据中学习的。我们的第一个结果是,最佳的通用的Tikhonov正规化工具,相对于平均的平方差差差差差,美元是随机的。我们发现,它完全独立于前方操作员$A1美元,只取决于美元的平均和通差。然后,我们考虑从两个不同框架内的有限培训中学习正规化器的问题:一个是监督的,基于美元和美元的样本,一个是不精确的, 仅基于更硬的, 美元的模型, 显示的是, 美元的平差的数值。