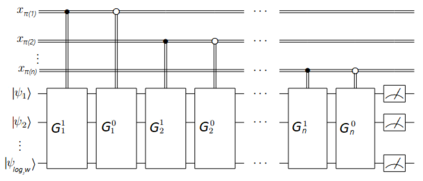
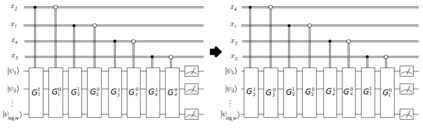
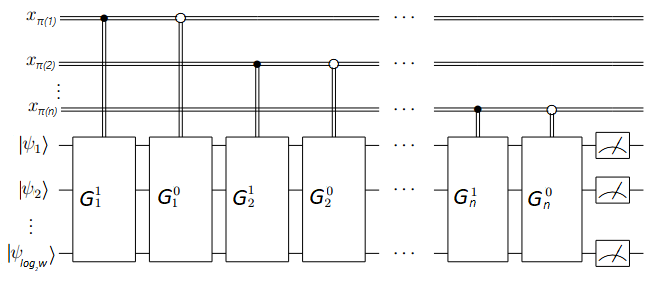
In this paper, we study quantum Ordered Binary Decision Diagrams($OBDD$) model; it is a restricted version of read-once quantum branching programs, with respect to "width" complexity. It is known that the maximal gap between deterministic and quantum complexities is exponential. But there are few examples of functions with such a gap. We present a new technique ("reordering") for proving lower bounds and upper bounds for OBDD with an arbitrary order of input variables if we have similar bounds for the natural order. Using this transformation, we construct a total function $REQ$ such that the deterministic $OBDD$ complexity of it is at least $2^{\Omega(n / \log n)}$, and the quantum $OBDD$ complexity of it is at most $O(n^2/\log n)$. It is the biggest known gap for explicit functions not representable by $OBDD$s of a linear width. Another function(shifted equality function) allows us to obtain a gap $2^{\Omega(n)}$ vs $O(n^2)$. Moreover, we prove the bounded error quantum and probabilistic $OBDD$ width hierarchies for complexity classes of Boolean functions. Additionally, using "reordering" method we extend a hierarchy for read-$k$-times Ordered Binary Decision Diagrams ($k$-$OBDD$) of polynomial width, for $k = o(n / \log^3 n)$. We prove a similar hierarchy for bounded error probabilistic $k$-$OBDD$s of polynomial, superpolynomial and subexponential width. The extended abstract of this work was presented on International Computer Science Symposium in Russia, CSR 2017, Kazan, Russia, June 8 -- 12, 2017
翻译:在本文中, 我们研究量定二进制( $OBDD$ ) 的量定二进制图解模式; 这是在“ 宽度” 复杂度方面, 限量的量定量分流程序。 已知确定性与量度复杂度之间的最大差距是指数指数指数指数指数指数。 但是, 很少有这样差的函数实例。 我们展示了一种新的技术( “ 重新排序” ), 证明OBDDD的下限和上界值, 如果对自然秩序有相似的参数, 并且是一个任意的输入序列。 使用这种转换, 我们构建了一个总值 $( $ 美元) 的读数, 它的确定性超级值 美元( 美元 美元 美元), 确定值的美元( 美元) 确定性等级( 美元), 并且 美元 数字( 美元) 数字( 数字- ) 数字( 数字- 数字- 数字- ) 的国际, 这是已知的明显功能的最大已知差距。