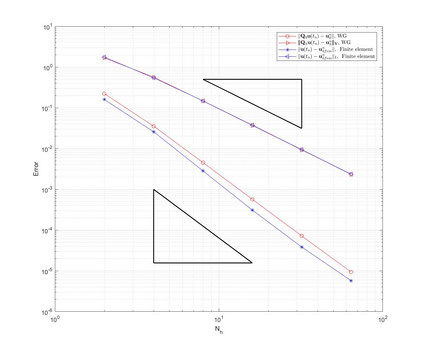
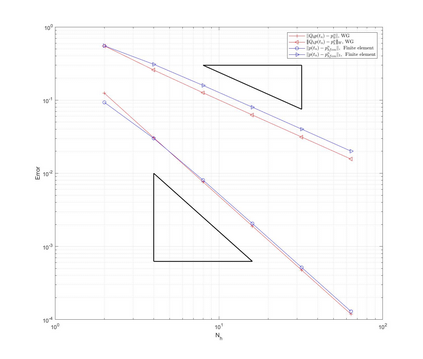
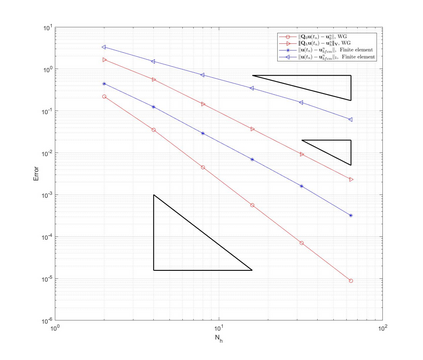
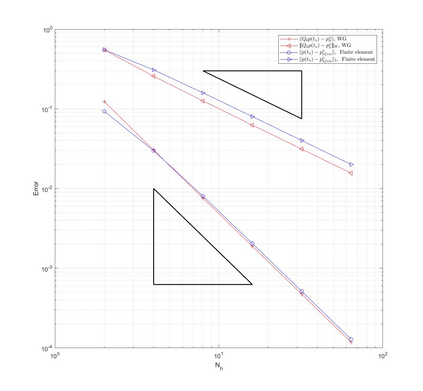
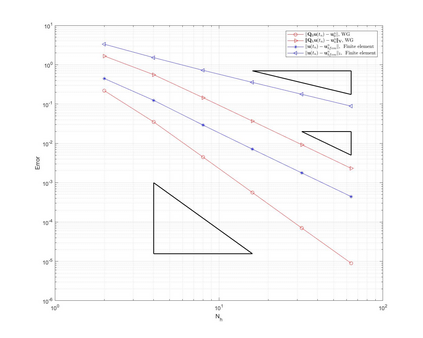
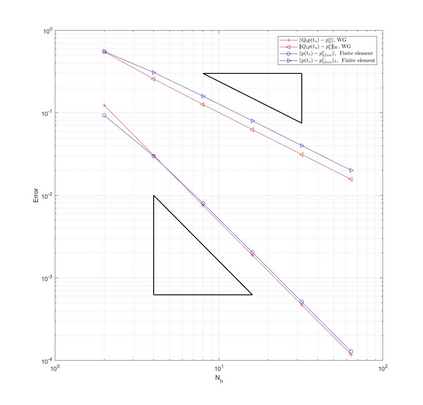
This paper is devoted to a weak Galerkin (WG) finite element method for linear poroelasticity problems where weakly defined divergence and gradient operators over discontinuous functions are introduced. We establish both the continuous and discrete time WG schemes, and obtain their optimal convergence order estimates in a discrete $H^1$ norm for the displacement and in an $H^1$ type and $L^2$ norms for the pressure. Finally, numerical experiments are presented to illustrate the theoretical error results in different kinds of meshes which shows the WG flexibility for mesh selections, and to verify the locking-free property of our proposed method.
翻译:本文专门论述对线性孔径问题采用较弱的Galerkin(WG)有限元素法,其中引入了定义薄弱的分歧和梯度操作者对不连续功能的偏差;我们制定了连续和离散时间WG办法,并按离散的1美元标准、1美元类型和2美元压力标准得出最佳汇合估计值;最后,提出了数字实验,以说明不同种类的网贝的理论错误结果,显示工作组对网目选择的灵活性,并核实我们拟议方法的无锁属性。