Model-based Kernel Sum Rule: Kernel Bayesian Inference with Probabilistic Models

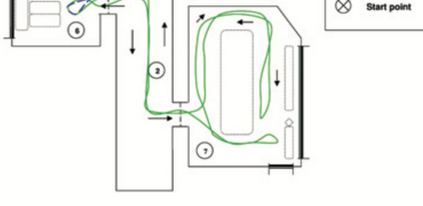
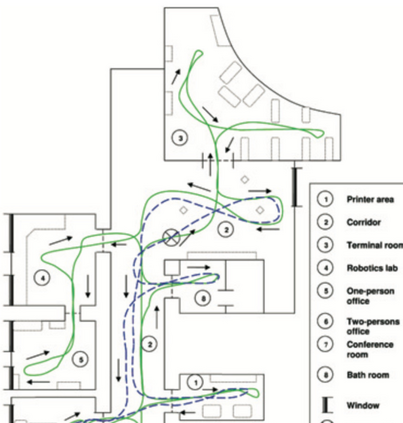
Kernel Bayesian inference is a principled approach to nonparametric inference in probabilistic graphical models, where probabilistic relationships between variables are learned from data in a nonparametric manner. Various algorithms of kernel Bayesian inference have been developed by combining kernelized basic probabilistic operations such as the kernel sum rule and kernel Bayes' rule. However, the current framework is fully nonparametric, and it does not allow a user to flexibly combine nonparametric and model-based inferences. This is inefficient when there are good probabilistic models (or simulation models) available for some parts of a graphical model; this is in particular true in scientific fields where "models" are the central topic of study. Our contribution in this paper is to introduce a novel approach, termed the {\em model-based kernel sum rule} (Mb-KSR), to combine a probabilistic model and kernel Bayesian inference. By combining the Mb-KSR with the existing kernelized probabilistic rules, one can develop various algorithms for hybrid (i.e., nonparametric and model-based) inferences. As an illustrative example, we consider Bayesian filtering in a state space model, where typically there exists an accurate probabilistic model for the state transition process. We propose a novel filtering method that combines model-based inference for the state transition process and data-driven, nonparametric inference for the observation generating process. We empirically validate our approach with synthetic and real-data experiments, the latter being the problem of vision-based mobile robot localization in robotics, which illustrates the effectiveness of the proposed hybrid approach.