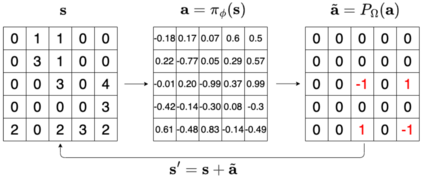
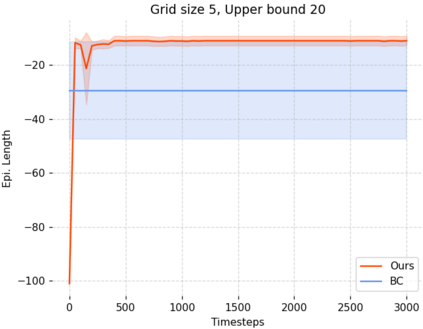
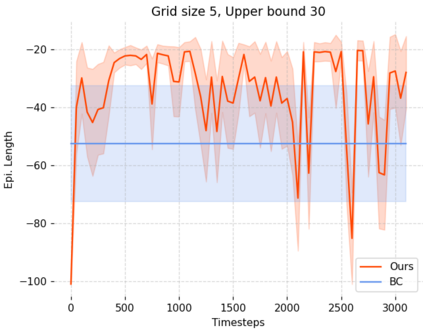
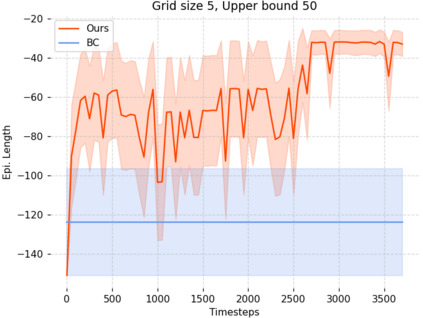
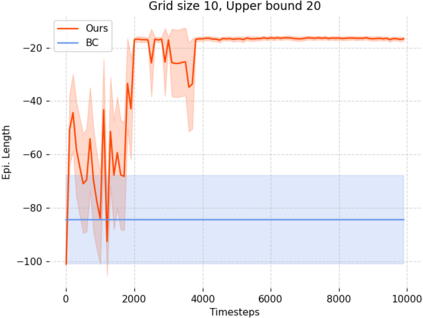
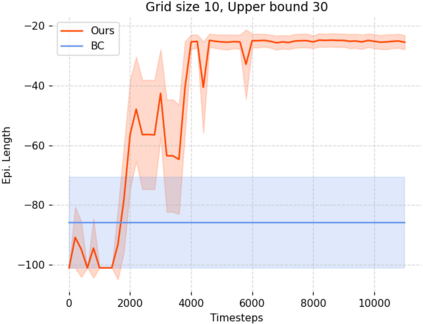
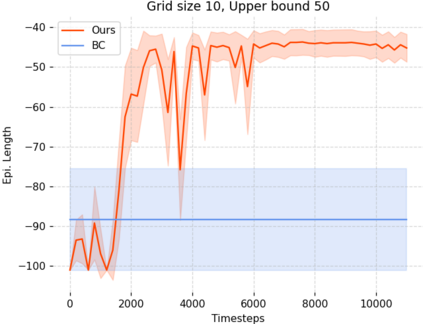
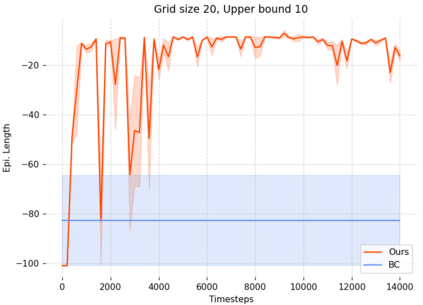
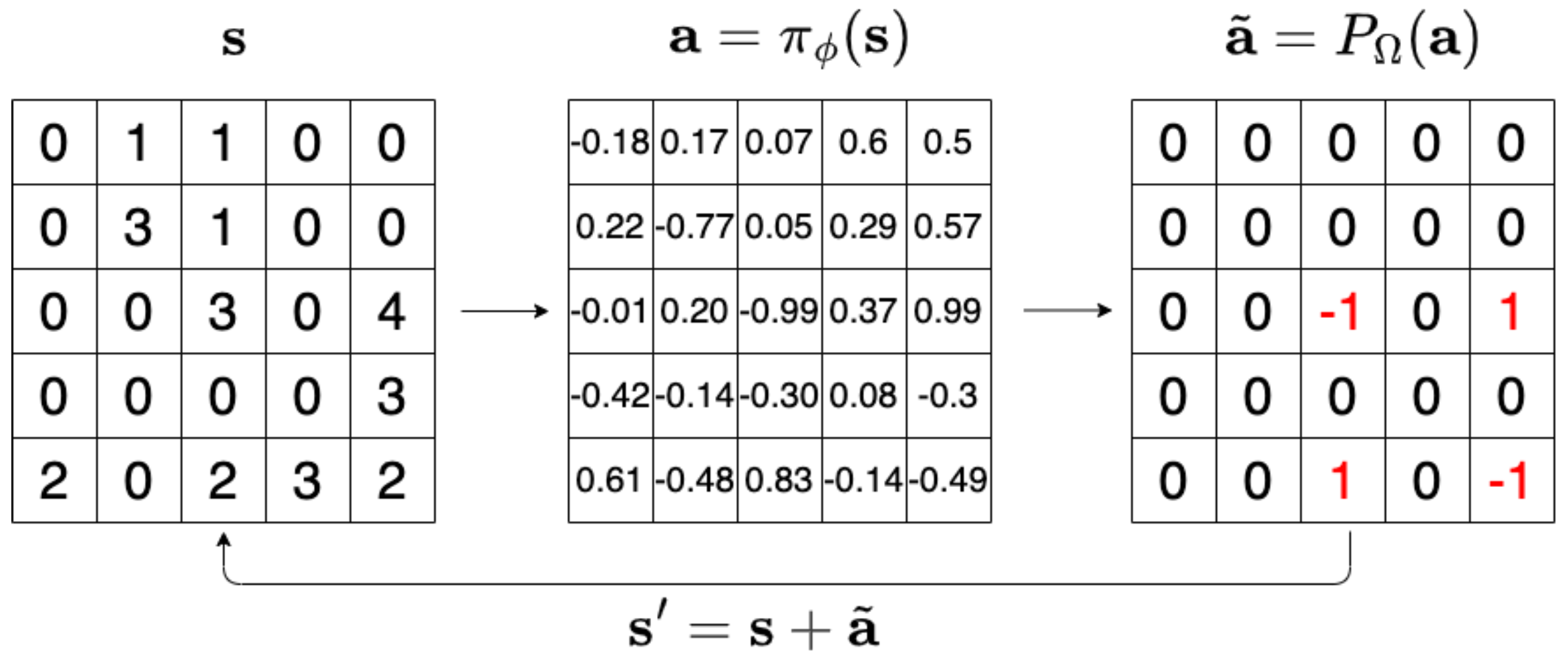
Can agents be trained to answer difficult mathematical questions by playing a game? We consider the integer feasibility problem, a challenge of deciding whether a system of linear equations and inequalities has a solution with integer values. This is a famous NP-complete problem with applications in many areas of Mathematics and Computer Science. Our paper describes a novel algebraic reinforcement learning framework that allows an agent to play a game equivalent to the integer feasibility problem. We explain how to transform the integer feasibility problem into a game over a set of arrays with fixed margin sums. The game starts with an initial state (an array), and by applying a legal move that leaves the margins unchanged, we aim to eventually reach a winning state with zeros in specific positions. To win the game the player must find a path between the initial state and a final terminal winning state if one exists. Finding such a winning state is equivalent to solving the integer feasibility problem. The key algebraic ingredient is a Gr\"obner basis of the toric ideal for the underlying axial transportation polyhedron. The Gr\"obner basis can be seen as a set of connecting moves (actions) of the game. We then propose a novel RL approach that trains an agent to predict moves in continuous space to cope with the large size of action space. The continuous move is then projected onto the set of legal moves so that the path always leads to valid states. As a proof of concept we demonstrate in experiments that our agent can play well the simplest version of our game for 2-way tables. Our work highlights the potential to train agents to solve non-trivial mathematical queries through contemporary machine learning methods used to train agents to play games.
翻译:代理商能否通过玩游戏来解答困难的数学问题? 我们考虑整数可行性问题, 即确定线性方程和不平等系统是否具有整数值解决方案的挑战。 这是数学和计算机科学许多领域的应用程序中著名的 NP 完成问题。 我们的论文描述了一个新的代数强化学习框架, 使代理商能够玩一个与整数可行性问题相等的游戏。 我们解释如何将整数可行性问题转换成一个游戏, 而不是一组带有固定差价的阵列。 游戏以初始状态( 阵列) 开始, 并应用一个使差位保持不变的法律动作来启动。 我们的目标是最终达到一个在特定位置上零位的赢家状态。 要赢得游戏必须在初始状态和最终结束状态之间找到一条路径。 我们的论文描述了一个新的代数强化框架, 使一个匹配状态能够解决整数的可行性问题。 我们的代数位化理想的基数基础是一个“ 硬基数基础 ”, 以初始状态( 阵列) 开始, 并且“ 硬基数” 基础可以被看成一个连接动作的组合状态, 在特定位置上, 游戏中, 我们的游戏中, 将一个预算到连续的游戏中, 我们的游戏中, 将不断的游戏的游戏的动力运动的动力移动到一个方向, 。